Fuerzas Conservativas
No todas las fuerzas se comportan igual desde el punto de vista energético. El trabajo que realizan sobre los cuerpos puede o no variar dependiendo del camino que siga el cuerpo en su desplazamiento. Este criterio será el que nos sirva para clasificar las fuerzas en conservativas y no conservativas o disipativas.
Definición de Fuerza Conservativa
Decimos que una fuerza es conservativa cuando el trabajo que realiza sobre un cuerpo depende sólo de los puntos inicial y final y no del camino seguido para llegar de uno a otro.
La definición anterior tiene varias implicaciones:
-
Sólo las fuerzas conservativas dan lugar a la energía potencial. El cálculo del trabajo realizado por fuerzas conservativas se reduce a una simple resta:
- El trabajo realizado por las fuerzas conservativas a lo largo de un camino cerrado es cero
- Cuando movemos un cuerpo venciendo una fuerza conservativa que se opone, el trabajo realizado aumenta la energía potencial del cuerpo
- Las fuerzas conservativas conservan la energía mecánica del sistema (por ejemplo la fuerza gravitatoria)
- Las fuerzas no conservativas o disipativas disipan la energía mecánica del sistema (por ejemplo la fuerza de rozamiento)
Ejemplo de Trabajo Realizado por Fuerza Conservativa
Vamos a calcular el trabajo realizado por la fuerza peso (fuerza gravitacional), que es una fuerza conservativa, en las tres situaciones de la figura, suponiendo que la fricción con el aire y con la rampa es cero.
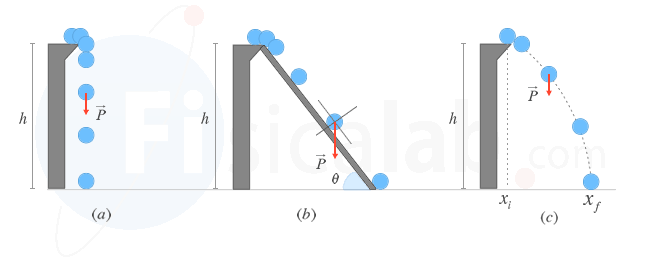
Figura a
- Fuerza que actúa:
- Desplazamiento:
Con los datos anteriores, calculamos el trabajo mediante la expresión:
Figura b
En este caso hemos de tener presente la nueva orientación del sistema de referencia.
- Fuerza que actúa:
- Desplazamiento:
Con los datos anteriores, calculamos el trabajo mediante la expresión:
Figura c
- Fuerza que actúa:
- Desplazamiento:
Con los datos anteriores, calculamos el trabajo mediante la expresión:
Conclusión
Como vemos, en los tres casos el trabajo realizado por la fuerza gravitacional es el mismo a pesar de que el cuerpo ha descrito trayectorias diferentes. Podemos concluir que la fuerza gravitacional es una fuerza conservativa, al depender el trabajo realizado por la misma únicamente de los puntos inicial y final.
Ejemplo de Trabajo Realizado por Fuerza no Conservativa
Vamos a calcular el trabajo realizado por la fuerza de rozamiento, que es una fuerza no conservativa o disipativa, en las dos situaciones de la figura. Se trata en ambos de un desplazamiento horizontal y el valor de la fuerza de rozamiento viene dado por
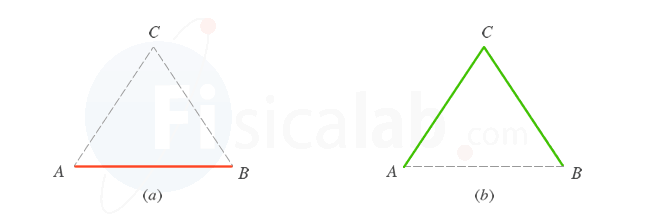
Figura a
En este caso vamos del punto A al punto B directamente.
- Fuerza estudiada:
- Desplazamiento:
Con los datos anteriores, calculamos el trabajo mediante la expresión:
Figura b
En este caso vamos del punto A al B pasando por el C. Dado que la distancia de cada lado es la misma que en el caso de la figura a, el trabajo realizado por la fuerza de rozamiento también será igual en cada tramo. Por tanto:
Conclusión
Como vemos, en cada uno de los casos el trabajo realizado por la fuerza de rozamiento es distinto. Podemos concluir que la fuerza de rozamiento no es conservativa sino disipativa, al depender el trabajo realizado por la misma de la trayectoria seguida por el cuerpo.
Fuerzas Centrales
Una parte importante de las fuerzas conservativas reciben el nombre de fuerzas centrales. Estas fuerzas se caracterizan porque:
- De manera independiente a la trayectoria que describa un cuerpo la dirección de su vector siempre apunta a un mismo punto.
- Su módulo depende de la distancia entre dicho punto y el cuerpo.
Las fuerzas centrales son fuerzas conservativas en las que su dirección se orienta siempre hacia un mismo punto fijo y su módulo depende de la distancia entre dicho punto fijo y su punto de aplicación.
Ejemplos importantes de este tipo de fuerzas son la fuerza gravitatoria de las leyes de Newton, la fuerza elástica de la ley de Hooke o la fuerza électrica de la ley de Coulomb.
Comprobación
A continuación vamos a comprobar que cualquier fuerza central es una fuerza conservativa. Para ello, vamos a tener en cuenta que cualquier movimiento entre dos puntos cualesquiera se puede descomponer en un conjunto de movimientos radiales y circulares. Partiendo de este hecho vamos a suponer que un cuerpo se mueve desde un punto A a otro B bajo la acción de una fuerza central
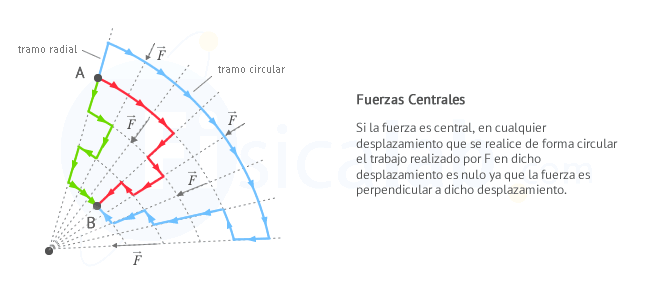
En cualquier desplazamiento que se realice de forma circular el trabajo realizado por
Teniendo en cuenta este último hecho podemos concluir sin temor a equivocarnos que cualquier fuerza central
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
