Aplicación segunda ley de Kepler

Datos

• Perihelio: r_P = 0.718 UA ( unidades astronómicas )
• Afelio: r_A = 0.728 UA
• Valor de la velocidad en el perihelio: v_P = 35.24 km/s 

Consideraciones previas

La siguiente imagen tiene los elementos fundamentales de la órbita elíptica de venús, representado en azul en distintos puntos, así como la representación de las magnitudes pedidas.

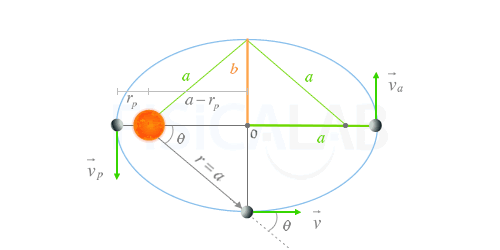
Resolución

En primer lugar, a partir de la imagen anterior, es inmediato que el eje mayor de la elipse ( 2·a ) es, justamente, la suma del perihelio y el afelio. Así, pues, nos queda:

$$r_P+r_A=2·a\Rightarrow a=\frac{r_P+r_A}{2}=\frac{0.718+0.728}{2}=0.723 \mathrm{UA}$$

Para determinar la velocidad en el afelio, a partir de la velocidad en el perihelio, podemos aplicar la segunda ley de Kepler, recordando que, al estar en los extremos de la elipse, el ángulo entre la velocidad y el vector de posición de Venus respecto al Sol es 90º. Así, nos queda:

$$r_P·v_P·\cancel{\sin \left({\theta }_P\right)}=r_A·v_A·\cancel{\sin \left({\theta }_A\right)}\Rightarrow v_A=\frac{r_P·v_P}{r_A}=\frac{0.718·35.24}{0.728}=34.75 km/s$$

Por último, para calcular la velocidad en el extremo del eje volvemos a aplicar la segunda ley de Kepler. De esta manera relacionamos la velocidad en dicho punto con la velocidad en el perihelio, por ejemplo. Hay que tener en cuenta que para calcular el ángulo que forma el vector velocidad y el vector de posición hay que recurrir a un poco de trigonometría. Observa:

$$r_P·v_P·\cancel{\sin \left({\theta }_P\right)}=r·v·\sin \left(\theta \right)$$

$$\cos \left(\theta \right)=\frac{a-r_P}{a}=\frac{0.723-0.718}{0.723}=0.0069\Rightarrow \theta =89.6º$$

$$\begin{gathered} r_P·v_P·\cancel{\sin \left({\theta }_P\right)}=r·v·\sin \left(\theta \right)\Rightarrow 0.718·35.24=0.723·v·\sin \left(89.6º\right)\Rightarrow \\ \Rightarrow v=34.99 km/s \end{gathered}$$

Observa que la órbita de Venús es prácticamente circular, lo que se traduce en una velocidad muy similar en cualquier punto estudiado.