Regla de L'Hôpital

La regla de L'Hôpital es un proceso que nos permite resolver algunas indeterminaciones que se dan en el cálculo de límites mediante el uso de las derivadas. En este apartado vamos a estudiar:

• El enunciado de la regla
• Su aplicación práctica
  • Indetermianciones 0/0
  • Indetermianciones ∞/∞
  • Indetermianciones 0·∞
  • Indetermianciones ∞-∞
  • Indetermianciones 1^∞, 0⁰ y ∞⁰
• Comprobación de la regla
• Interpretación geométrica de la misma

¡Vamos con ello!

Enunciado

La regla anterior se puede aplicar también, gracias a un cambio de variable, cuando tenemos x→∞. Es decir, si tenemos dos funciones derivables, f(x) y g(x), y sabemos que $\underset{x\to \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\left[\frac{0}{0}\right]$ y $\underset{x\to \infty }{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}=L$, entonces:

$$\boxed{\underset{x\to \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to \infty }{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}=L}$$

Comprobación de aplicación cuando x→∞

Haciendo x=1/t, tenemos que cuando x→∞, t→0⁺, y por tanto:

$${\displaystyle \begin{array}{c}\underset{x\to \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\left[\frac{0}{0}\right]\\ \underset{x\to \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{t\to 0^{+}}{\lim }\frac{f\left({\displaystyle \frac{1}{t}}\right)}{g\left({\displaystyle \frac{1}{t}}\right)}=\left[\frac{0}{0}\right]\end{array}}$$

En estas condiciones podemos aplicar la regla de L'Hôpital tal y como la habíamos enunciado:

$$\underset{x\to \infty }{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{t\to 0^{+}}{\lim }\frac{f\left({\displaystyle \frac{1}{t}}\right)}{g\left({\displaystyle \frac{1}{t}}\right)}\underset{L\text{'}H+ \text{regla cadena}}{=}\underset{t\to 0^{+}}{\lim }\frac{\left(-1/t^2\right)·f\text{'}\left({\displaystyle \frac{1}{t}}\right)}{\left(-1/t^2\right)·g\text{'}\left({\displaystyle \frac{1}{t}}\right)}=\underset{t\to 0^{+}}{\lim }\frac{f\text{'}\left({\displaystyle \frac{1}{t}}\right)}{g\text{'}\left({\displaystyle \frac{1}{t}}\right)}\underset{x=\frac{1}{t}}{=}\underset{x\to \infty }{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}$$

En resumidas cuentas, podemos aplicar la regla tanto en el caso de que x→a como en x→∞.

Tres últimas consideraciones antes de estudiar algunos ejemplos prácticos:

Marqués de L'Hôpital

Guillaume François Antoine (1661 – 1704)​, más conocido como el marqués de L'Hôpital, fue un matemático francés nacido en París que se especializó en el análisis matemático. Uno de sus profesores fue Johann Bernoulli, y se cree que fue en realidad este último el descubridor de la regla de L'Hôpital.

​

Bernoulli y L'Hôpital habrían llegado a un trato en 1694 por el cual Bernoulli le transmitiría sus conocimientos a L'Hôpital. Este último describió dichos descubrimientos en el primer libro conocido de cálculo diferencial: Análisis de los infinitamente pequeños para el entendimiento de las líneas curvas.

Aplicaciones prácticas

Indeterminaciones del tipo [0/0]

Se trata del caso directo que hemos visto en la definición de la propia regla, y, como ya sabes, la puedes aplicar tanto en x→a como en x→∞.

Ejemplo

$$\begin{gathered} \underset{x\to 2}{\lim }\frac{x^2-x-2}{3x^2+3x-18}=\left[\frac{0}{0}\right]\text{IND} \\ \underset{x\to 2}{\lim }\frac{x^2-x-2}{3x^2+3x-18}\underset{L\text{'}H}{=}\underset{x\to 2}{\lim }\frac{2x-1}{6x+3}=\frac{3}{15}=\frac{1}{5} \end{gathered}$$

Indeterminaciones del tipo [∞/∞]

Las indeterminaciones del tipo (±∞/±∞) se pueden transformar en indeterminaciones del tipo (0/0), sin más que hacer una doble inversión, de ahí que también se pueda aplicar la regla para este tipo de indeterminaciones, tanto en x→a como en x→∞.

Ejemplo

$$\underset{x\to \infty }{\lim }\frac{3x}{2x}=\underset{x\to \infty }{\lim }\frac{{\displaystyle \frac{1}{2x}}}{{\displaystyle \frac{1}{3x}}}\underset{L\text{'}H}{=}\left\{\begin{array}{l}\underset{x\to \infty }{\lim }\frac{\left(3x\right)\text{'}}{\left(2x\right)\text{'}}=\underset{x\to \infty }{\lim }\frac{3}{2}=\frac{3}{2}\\ \underset{x\to \infty }{\lim }\frac{{\displaystyle \left(\frac{1}{2x}\right)\text{'}}}{{\displaystyle \left(\frac{1}{3x}\right)\text{'}}}=\underset{x\to \infty }{\lim }\frac{-{\displaystyle \frac{1}{2\cancel{x^2}}}}{-{\displaystyle \frac{1}{3\cancel{x^2}}}}=\frac{3}{2}\end{array}\right.$$

Indeterminaciones del tipo [0·∞]

Las indeterminaciones del tipo (0·∞) se pueden transformar en indeterminaciones del tipo (0/0) ó (∞/∞), sin más que hacer una inversión, de ahí que también se pueda aplicar la regla para este tipo de indeterminaciones, tanto en x→a como en x→∞. Observa que:

$$0·\infty =\left\{\begin{array}{l}0·\frac{\mathbf{1}}{{\displaystyle \frac{\mathbf{1}}{\mathbf{\infty }}}}=\frac{0}{0}\\ \frac{\mathbf{1}}{{\displaystyle \frac{\mathbf{1}}{\mathbf{0}}}}·\infty =\frac{\infty }{\infty }\end{array}\right.$$

Ejemplo

$$\begin{array}{c}\underset{x\to 0}{\lim }x·\log \left(x\right)=\left[0·\infty \right]\text{IND}\\ \underset{x\to 0}{\lim }x·\log \left(x\right)=\underset{x\to 0}{\lim }\frac{1}{{\displaystyle \frac{1}{x}}}·\log \left(x\right)\underset{L\text{'}H}{=}\underset{x\to 0}{\lim }\frac{1/x}{-{\displaystyle \frac{1}{x^2}}}=\underset{x\to 0}{\lim }\left(-x\right)=0\end{array}$$

Indeterminaciones del tipo [∞-∞]

Es habitual que podamos convertir este tipo de indeterminaciones en cualquiera de las anteriores operando la función que resulta en la indeterminación, o multiplicando y dividiendo por el conjugado.

Ejemplo

$$\underset{x\to \infty }{\lim }x-\sqrt{x^2-3x}=\left[\infty -\infty \right]\text{IND}$$

Si multiplicamos y dividimos por el conjugado el valor de la función no varía (sería lo mismo que multiplicar y dividir por un número cualquiera), pero vamos adaptando la función al tipo de indeterminación que necesitamos. Observa:

$$\underset{x\to \infty }{\lim }x-\sqrt{x^2-3x}=\underset{x\to \infty }{\lim }\frac{\left(x-\sqrt{x^2-3x}\right)·\left(x+\sqrt{x^2-3x}\right)}{\left(x+\sqrt{x^2-3x}\right)}\underset{\left(a+b\right)\left(a-b\right)=a^2-b^2}{=}\underset{x\to \infty }{\lim }\frac{x^2-x^2+3x}{\left(x+\sqrt{x^2-3x}\right)}=\left[\frac{\infty }{\infty }\right]\text{IND}$$

Hasta aquí no hemos aplicado L'Hôpital. Ahora sí, resolvemos derivando numerador y denominador:

$$\underset{x\to \infty }{\lim }\frac{3x}{\left(x+\sqrt{x^2-3x}\right)}\underset{L\text{'}H}{=}\underset{x\to \infty }{\lim }\frac{3}{\left(1+\underset{M}{\underbrace{{\displaystyle \frac{2x-3}{2\sqrt{x^2-3x}}}}}\right)}$$

Resolvemos aparte el límite M:

$$M=\underset{x\to \infty }{\lim }\frac{2x-3}{2\sqrt{x^2-3x}}=\underset{x\to \infty }{\lim }\frac{{\displaystyle \frac{2x}{x}}-{\displaystyle \frac{3}{x}}}{2\sqrt{{\displaystyle \frac{x^2}{x^2}}-{\displaystyle \frac{3x}{x^2}}}}=\frac{2}{2}=1$$

Donde hemos dividido todo el numerador y todo el numerador por la potencia de mayor grado del denominador, x, que al entrar en la raíz se convierte en x². Volviendo al límite anterior nos queda:

$$\underset{x\to \infty }{\lim }\frac{3}{\left(1+\underset{M}{\underbrace{{\displaystyle \frac{2x-3}{2\sqrt{x^2-3x}}}}}\right)}=\underset{x\to \infty }{\lim }\frac{3}{\left(1+1\right)}=\frac{3}{2}$$

Indeterminaciones del tipo [1^∞], [0⁰] y [∞⁰]

En estos casos se trata de asumir que el límite existe y su valor es L (por ejemplo), tomar logaritmos y aplicar L'H.

Ejemplo

$$\begin{gathered} \underset{x\to 0}{\lim }{\left(\frac{3^x+e^x}{2}\right)}^{\frac{1}{x}}={\left(\frac{2}{2}\right)}^{\infty }=\left[1^{\infty }\right]\text{IND} \\ L=\underset{x\to 0}{\lim }{\left(\frac{3^x+e^x}{2}\right)}^{\frac{1}{x}}\Rightarrow \ln \left(L\right)=\ln \left(\underset{x\to 0}{\lim }{\left(\frac{3^x+e^x}{2}\right)}^{\frac{1}{x}}\right) \end{gathered}$$

Podemos aplicar las propiedades de los logaritmos, y recordar que ln(a)^b=b·ln(a), con lo que...

$$\begin{gathered} \ln \left(L\right)=\ln \left(\underset{x\to 0}{\lim }{\left(\frac{3^x+e^x}{2}\right)}^{\frac{1}{x}}\right)=\underset{x\to 0}{\lim }\frac{\ln \left(\frac{3^x+e^x}{2}\right)}{x}=\left[\frac{0}{0}\right]\text{IND} \\ \ln \left(L\right)=\underset{x\to 0}{\lim }\frac{\ln \left(\frac{3^x+e^x}{2}\right)}{x}\underset{L\text{'}H}{=}\underset{x\to 0}{\lim }\frac{{\displaystyle \frac{{\displaystyle \frac{3^x\ln \left(3\right)+e^x}{\cancel{2}}}}{\frac{3^x+e^x}{\cancel{2}}}}}{1}=\underset{x\to 0}{\lim }\frac{{\displaystyle 3^x\ln \left(3\right)+e^x}}{3^x+e^x}=\frac{\ln \left(3\right)+1}{2} \end{gathered}$$

Por tanto...

$$\ln \left(L\right)=\frac{\ln \left(3\right)+1}{2}\Rightarrow L=e^{\frac{\ln \left(3\right)+1}{2}}$$

Comprobación

Se trata de demostrar que para dos funciones derivables en un entorno de a que cumplen que...

1. $\underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\left[\frac{0}{0}\right]$
2. $\underset{x\to a}{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}=L$

...se verifica que:

$$\underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a}{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}=L$$

De (1) sabemos que g(a)=0. De (2) sabemos que g'(x)≠0 en un entorno de a. Esto último implica que la función será creciente o decreciente en un entorno de a, según g'(x)>0 o g'(x)<0. En cualquier caso, g(x)≠0 en un entorno de a.

Por otro lado, de (1) también sabemos que f(a)=0. Así pues, podemos escribir que:

$$\frac{f\left(x\right)}{g\left(x\right)}=\frac{f\left(x\right)-f\left(a\right)}{g\left(x\right)-g\left(a\right)}$$

Ya que, al restar 0 al numerador y al denominador el cociente no va a cambiar. Sin embargo, ahora estamos tenemos una expresión sobre la que aplicar el teorema de Cauchy. Así, si tomamos un entorno de a, para cualquier x∈(x₁, x₂), con x≠a existiría un valor c_x en el intervalo (x₁, x₂) tal que:

$$\frac{f\left(x\right)}{g\left(x\right)}=\frac{f\left(x\right)-f\left(a\right)}{g\left(x\right)-g\left(a\right)}=\frac{f\text{'}\left(c_x\right)}{g\text{'}\left(c_x\right)}$$

Cuando x→a, c_x también tiende a a, con lo que podemos escribir:

$$\underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}=\underset{x\to a}{\lim }\frac{f\left(x\right)-f\left(a\right)}{g\left(x\right)-g\left(a\right)}=\underset{x\to a}{\lim }\frac{f\text{'}\left(c_x\right)}{g\text{'}\left(c_x\right)}=\underset{x\to a}{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}=L$$

Esta última afirmación de paso al límite, si bien es cierta, requeriría de una demostración más rigurosa que queda fuera del alcance de este nivel.

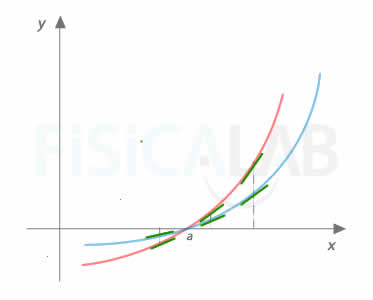
Interpretación geométrica

La regla de L'Hôpital puede ser entendida intuitivamente al relacionar las gráficas de f, g y sus derivadas. Veámoslo en la siguiente simulación.

Experimenta y Aprende

Cargando...

Interpretación gráfica de la regla de L'Hôpital

En la figura se muestran dos funciones f(x) y g(x). En general, si $\exists \underset{x\to a}{\lim }\frac{f\left(x\right)}{g\left(x\right)}$, quiere decir que la relación entre las ordenadas de ambas funciones tiende a estabilizarse a medida que nos aproximamos a a.

Por otro lado, si $\exists \underset{x\to a}{\lim }\frac{f\text{'}\left(x\right)}{g\text{'}\left(x\right)}$, lo que tiende a estabilizarse es la relación entre sus pendientes, marcadas en verde en la figura.

Como puedes apreciar en la imagen, la relación entre las pendientes, en el límite, es igual a la relación entre las funciones.

Pulsa sobre el botón play para comprobarlo tú mismo.