Derivabilidad y Continuidad
Una función f(x) es derivable en un punto, cuando existe la derivada f'(x) de la función en ese punto.
En la mayoría de casos prácticos que estudiarmos en este nivel educativo, para saber si una función f(x) es derivable en x=a puedes comprobar que:
Es decir, puedes comprobar que f'(a) es continua en x=a. No obstante, una función puede ser derivable (
En este apartado vamos a estudiar:
- La relación entre derivabilidad y continuidad
- Qué es el dominio de derivabilidad
- Cómo estudiar la derivabilidad de funciones a trozos
¿Empezamos?
Relación con la continuidad
De apartados anteriores sabes que la derivada de una función en un punto x=a, f'(a) se define según:
Para que exista ese límite, deben existir y coincidir los límites laterales correspondientes, es decir
Por otro lado, decimos que una función es continua en x=a cuando:
Pues bien, existe una relación entre continuidad y derivabilidad de una función.
Si una función es derivable en un punto, entonces es continua en él. Sin embargo, una función puede ser continua en un punto pero no derivable en él.
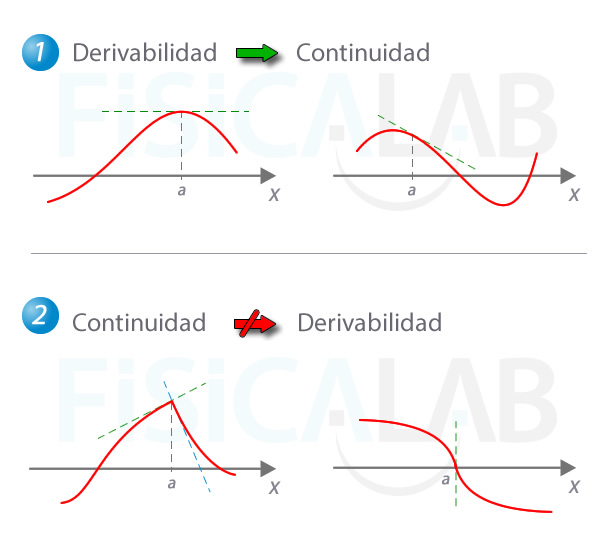
Interpretación gráfica
Las dos funciones superiores, en 1, son derivables en el punto considerado x=a. La pendiente de la curva, representada por la recta tangente en verde discontinuo, varía de manera suave. Todas las funciones derivables en un punto son continuas en él. Abajo, en 2 tenemos dos funciones continuas. En la de la izquierda hay un punto anguloso, y la de la derecha presenta una recta tangente vertical en el punto considerado. Ambos son ejemplos de funciones continuas no derivables.
Demostración
Partiendo de que
Comenzamos reescribiendo la condición de continuidad:
Por otro lado, sabemos que:
Tomando el límite cuando h tiende a 0 en ambos miembros de la expresión anterior obtenemos:
Ahora, el límite del producto es el producto de los límites, con lo que:
Con lo que...
Como -f(a) no depende de h, podemos "sacarla" fuera del límite, quedando finalmente:
Decimos que una función es derivable en un intervalo cuando lo es en todos los puntos del mismo.
Dominio de derivabilidad
Se trata de un concepto importante relacionado con la derivabilidad de una función.
Llamamos dominio de derivabilidad al conjunto de puntos en los que una función es derivable. Se cumple que, en general, es un subconjunto del dominio de la función original:
Para calcular el dominio de derivabilidad simplemente calculamos el dominio de la función derivada.
Ten presente que una función no es derivable en los extremos del intervalo en el que está definida, si estos son un valor finito. Así, por ejemplo, la función
Observa que el 0, en el extremo inferior del dominio, no pertenece al dominio de derivabilidad, a pesar de pertenecer al dominio.
Efectivamente, tú mismo podrías haber llegado a esta conclusión al observar que el dominio de la función derivada de
...es justamente (0,∞)
Derivabilidad de una función a trozos
Un caso de particular interés en el estudio de la derivabilidad es cuando una función está definida a trozos, es decir, mediante diferentes expresiones según la rama. En este tipo de funciones hemos de asegurarnos que:
- La función f(x) es continua
- La función no presenta un punto anguloso
Así pues, para estudiar la derivabilidad de una función a trozos en el cambio de rama puedes seguir los siguientes pasos:
- Estudiamos la continuidad en el cambio de rama (supongamos que dicho cambio se produce en x=a)
- Si la función no es continua, tampoco es derivable en el cambio de rama
- Si la función es continua, estudiamos las derivadas laterales
- Si son finitas y coinciden, la función es derivable en el punto considerado, y el valor de la derivada en el cambio de rama, f'(a), es precisamente el de las derivadas laterales
- Si no coinciden la función no es derivable en el cambio de rama, es decir, no existe f'(a)
No olvides comprobar, si fuera preciso, la derivabilidad en el resto de puntos del dominio. ¡Visita los ejercicios asociados a este apartado para profundizar en todo ello!
Ejemplo
Si nos pidiesen calcular la derivabilidad y el dominio de derivabilidad de la función valor absoluto, tenemos:
Se trata de buscar los puntos problemáticos para la derivabilidad. En este caso, el punto que puede presentar problemas de derivabilidad es x=0. Aunque la función es continua en él...
...las derivadas laterales en él no coinciden:
Con lo que la función no es derivable en x=0 y no existe f'(0). Por tanto:
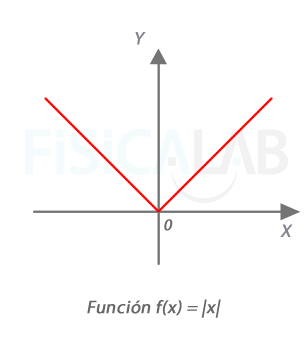
Dominio de derivabilidad en función valor absoluto
La función valor absoluto de x es continua en todos los reales, pero presenta un punto anguloso en x=0 que hace que no sea derivable en él, quedando por tanto excluido del dominio de derivabilidad.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
