Dominio de una Función

Una función es una relación entre dos conjuntos, en la que a cada valor del primer conjunto, denominado dominio, le corresponde un único valor del segundo, denominado recorrido.

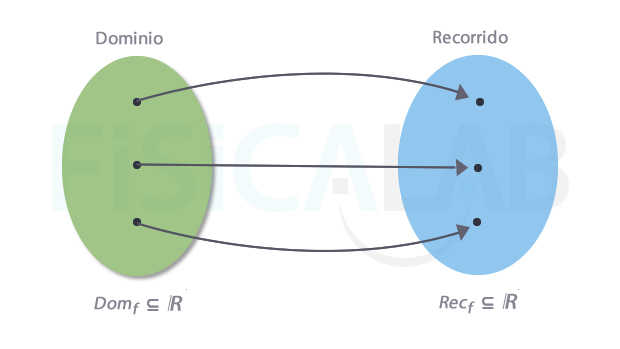
Dominio en funciones reales

Al igual que los dominios de los reyes de la antigüedad marcaban el alcance del poder y la autoridad de los mismos, en el mundo de las funciones, el dominio marca el conjunto de elementos sobre los cuales cada función puede actuar. En una función real de variable real tanto el dominio como el recorrido forman parte del conjunto de los números reales. Cada elemento del dominio se ilustra en la imagen por un punto negro sobre fondo verde, y cada elemento del recorrido como un punto negro sobre fondo azul. Las flechas indican la correspondencia entre unos y otros a través de la función.

Aunque ya hemos introducido este concepto en apartados anteriores, en este vamos a profundizar en su estudio para el caso de las funciones reales, y aprenderemos a calcularlo. Lo haremos a través de los siguientes puntos:

Definición
Restricciones del dominio
Cálculo del dominio

¿Preparado para extender el dominio de tus conocimientos?

Definición

El dominio de una función real, también llamado dominio de definición o campo de existencia de la misma, es el conjunto de elementos para los cuales la función está definida. Dicho de otra manera, el subconjunto de los números reales que tienen imagen. Formalmente:

D o m_{f} = \{x \in ℝ / \exists y = f (x) \in ℝ\}

Dom_f : Es el dominio de la función. También se puede denotar por Dom(f) o, simplemente, D. Puede ser todo el conjunto de los números reales, o bien un subconjunto de este: $D o m_{f} \subseteq ℝ$
x : Es un número real, perteneciente al dominio de la función, que recibe el nombre de variable independiente
y : Es otro número real, perteneciente al conjunto imagen de la función, que recibe el nombre de variable dependiente. Su valor se obtiene aplicando la función f al valor de x : y=f(x) . Para un par de valores concretos (x,y) decimos que y es la imagen de x, y que x es la antiimagen de y

Recuerda el significado de los siguientes símbolos:

∃ existe un
∀ para todo
∈ pertenece a
/ tal que
⊂ subconjunto de
⊆ subconjunto o igual a

Restricción

El dominio forma parte de la propia definición de una función. Recuerda:

$\begin{matrix} f : & D o m_{f} & \to & ℝ \\ x & \mapsto & y = f (x) \end{matrix}$

Sin embargo, no es habitual dar las funciones de esta manera. Como hemos hablado en apartados anteriores, en general verás las funciones reales escritas como ecuaciones matemáticas y tendrás que ser tú mismo el que "deduzca" el dominio. Este será, o bien todo el conjunto de los reales $D o m_{f} = ℝ$ , o bien un subconjunto de este $D o m_{f} \subset ℝ$ (con lo que podemos escribir que, en general, $D o m_{f} \subseteq ℝ$ ).

Puede restringirse el dominio por las siguientes razones:

Cuando sea matemáticamente imposible realizar alguna operación con ciertos valores x
Cuando el contexto real del que se ha obtenido la función así lo determine
Cuando lo necesitemos por alguna otra razón

Vamos a centrarnos en el primer caso, viendo cómo restringir de manera concreta el dominio, según el tipo de función.

Cómo calcular el dominio

Para calcular el dominio "quitaremos" de la ecuación aquellos valores que hagan imposible realizar alguna operación matemática.

Funciones polinómicas

*Expresión general*	*Ejemplos*
$f (x) = c_{0} + c_{1} \cdot x + c_{2} \cdot x^{2} + \dots + c_{n} \cdot x^{n}$	$f (x) = 3 g (x) = 2 + 3 x h (x) = 2 + 3 x - 5 x^{3}$

El dominio es $ℝ$ ya que al sustituir un número real cualquiera $x \in ℝ$ , siempre va a existir f(x).

Gráficas de funciones polinómicas: constante, lineal, cuadrática y cúbica

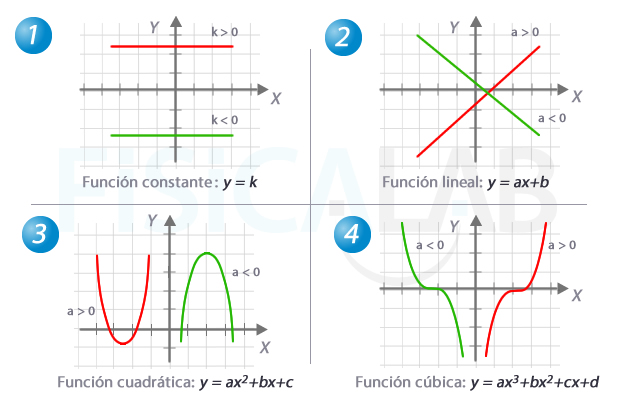
Funciones polinómicas habituales

En la ilustración las 4 funciones polinómicas más habituales. Observa como dependiendo del valor que acompaña a la x de mayor grado, la función presenta unas características particulares.

Funciones racionales

*Expresión general*	*Ejemplos*
$f (x) = \frac{P (x)}{Q (x)}$	$f (x) = \frac{1}{x} g (x) = \frac{2 + 3 x}{x} h (x) = \frac{2 + 3 x - 5 x^{3}}{2 + 3 x^{5}}$

El denominador debe ser distinto de cero. Si P(x) y Q(x) son polinomios, entonces el dominio es $D o m_{f} = \{x \in ℝ / Q (x) \neq 0\}$ , es decir, el conjunto de valores que no anulan el denominador.

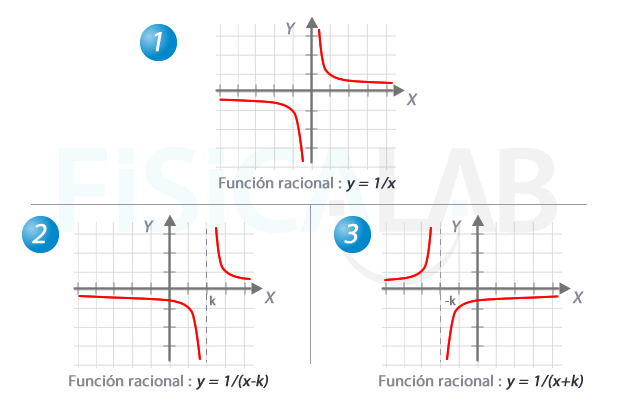
Funciones racionales

El caso más simple de función racional es el de la función de proporcionalidad inversa 1/x. En ese caso, la gráfica resulta una hipérbola equilátera. Restando o sumando una constante k al denominador desplazamos la gráfica hacia la izquierda o la derecha respectivamente.

Cuando simplifiques una función racional el dominio debe coincidir con el de la función original, y no debes caer en la tentación de recalcularlo.

Efectivamente, observa el siguiente ejemplo:

$f (x) = \frac{x^{2} - 1}{x + 1} = \frac{(x + 1) (x - 1)}{x + 1} = x - 1$

Tanto la función original como la simplificada deben tener las mismas imágenes. Esto es evidente para cualquier valor "no problemático", por ejemplo el 3:

$f (3) = \frac{3^{2} - 1}{3 + 1} = 2; f (3) = 2 - 1 = 2$

Sin embargo, en los valores que restringen el dominio de la función original el comportamiento varía:

$f (- 1) = \frac{{(- 1)}^{2} - 1}{- 2 + 1} = \frac{0}{0} No existe; f (- 1) = - 1 - 1 = - 2$

De ahí que tales valores se quiten del dominio, aunque la función se simplifique.

Funciones irracionales

Cabe distinguir aquellas raíces de índice impar de las de índice par.

*Expresión general*	Ejemplos n impar	Ejemplos n par
$f (x) = \sqrt[n]{r (x)}$	$f (x) = \sqrt[3]{x} g (x) = \sqrt[5]{2 + 3 x} h (x) = \sqrt[127]{5 x^{18}}$	$f (x) = \sqrt{x} g (x) = \sqrt[6]{2 + 3 x} h (x) = \sqrt[128]{5 x^{18}}$

Función irracional de índice impar

En estos casos, la raíz no impone ninguna restricción adicional al dominio, con lo que coincidirá con el del radicando r(x). Si r(x) es un polinomio, entonces: $D o m_{f} = ℝ$ .

Función irracional de índice par

En estos casos la raíz impone que los valores del radicando r(x) siempre sean mayores o iguales que cero. Si r(x) es un polinomio, entonces: $D o m_{f} = \{x \in ℝ / r (x) ⩾ 0\}$

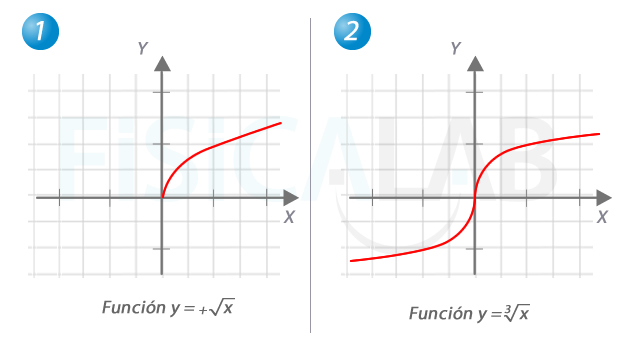
Funciones raíz

Las raíces de índice par, como la raíz cuadrada de la izquierda, tienen como dominio solo los valores positivos de x. En el caso de las raíces de índice impar, como la raíz cúbica de la derecha, todos los reales tienen imagen.

Funciones exponenciales

*Expresión general*	*Ejemplos*
$f (x) = a^{e (x)}$	$f (x) = 2^{x} g (x) = e^{3 x + 2} h (x) = 10^{- x^{2} + x - 2}$

En estos casos, la exponencial no impone ninguna restricción adicional al dominio, con lo que coincidirá con el del exponente e(x). Si e(x) es un polinomio, entonces: $D o m_{f} = ℝ$ .

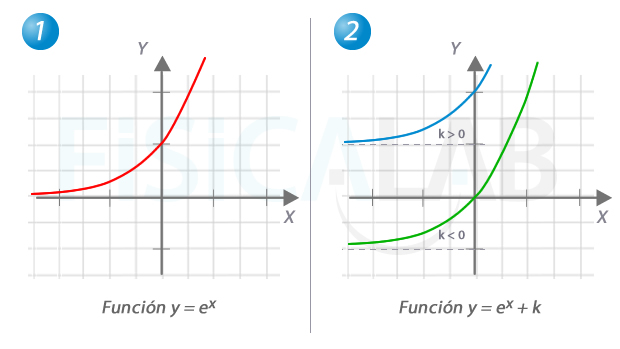
Funciones exponenciales

Una función muy habitual en la naturaleza es la exponencial e^x representada en 1. El número e es un número irracional, como por ejemplo lo es π, y cuyo valor es aproximadamente igual a 2,7182. Restando o sumando una constante k a la función exponencial, desplazamos la gráfica hacia la arriba o hacia abajo respectivamente, como se ilustra en 2.

Funciones logarítmicas

*Expresión general*	*Ejemplos*
$f (x) = \log_{n} (a (x))$	$f (x) = \log_{3} (9 x^{3} + 2) g (x) = \log_{10} (x) \Rightarrow g (x) = \log (x) h (x) = \log_{e} (x - 5) \Rightarrow h (x) = \ln (x - 5)$

En estos casos el logaritmo impone que el argumento a(x) sea un número positivo. Si a(x) es un polinomio, entonces: $D o m_{f} = \{x \in ℝ / a (x) > 0\}$ .

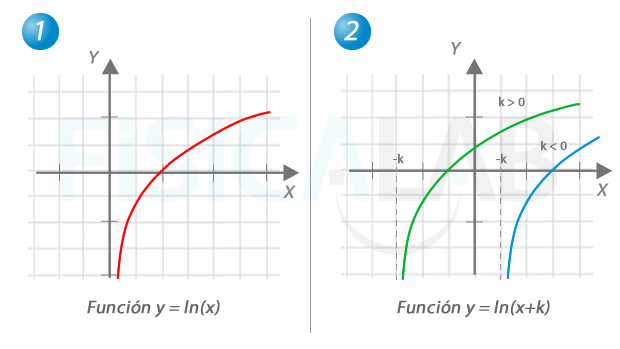
Funciones logarítmicas

La función logaritmo neperiano, a la izquierda, es una función logarítmica en la que la base es el número e (de ahí que sea la función recíproca de la exponencial de base e ). Restando o sumando una constante k a la variable independiente, desplazamos la gráfica hacia la derecha o la izquierda respectivamente, haciendo que el dominio comience en -k en lugar de 0, como se ilustra en 2.

Función seno

*Expresión general*	*Ejemplos*
$f (x) = \sin (a (x))$	$f (x) = \sin (x) g (x) = \sin (3 x^{2} + 2) h (x) = \sin (- 5 x + x^{3})$

En estos casos el seno no impone ninguna restricción adicional al dominio, con lo que coincidirá con el del argumento a(x). Si a(x) es un polinomio, entonces: $D o m_{f} = ℝ$ .

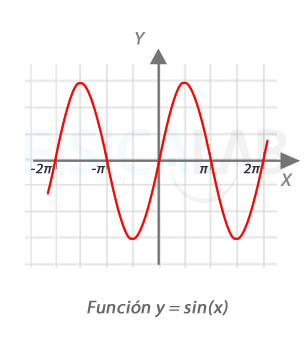
Funciones seno

En la ilustración, la gráfica de la función seno ( abreviado sin(x), del latín sinus ). Dicha función no impone ninguna restricción al dominio: cualquier valor real tiene imagen.

Función coseno

*Expresión general*	*Ejemplos*
$f (x) = \cos (a (x))$	$f (x) = \cos (x) g (x) = \cos (3 x^{2} + 2) h (x) = \cos (- 5 x + x^{3})$

En estos casos el coseno tampoco impone ninguna restricción adicional al dominio, con lo que coincidirá con el del argumento a(x). Si a(x) es un polinomio, entonces: $D o m_{f} = ℝ$ .

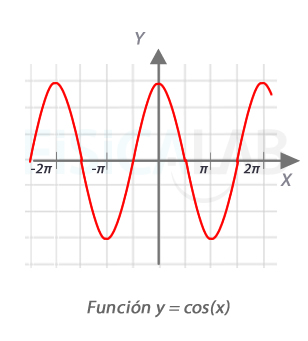
Funciones coseno

En la ilustración, la gráfica de la función coseno ( abreviado cos(x) ). Dicha función no impone ninguna restricción al dominio: cualquier valor real tiene imagen.

Función tangente

*Expresión general*	*Ejemplos*
$f (x) = \tan (a (x))$	$f (x) = \tan (x) g (x) = \tan (3 x^{2} + 2) h (x) = \tan (- 5 x + x^{3})$

En estos casos es bueno recordar que la tangente se define como $\tan (a (x)) = \frac{\sin (a (x))}{\cos (a (x))}$ , con lo que impone que el valor del argumento a(x) no sea un múltiplo impar de π/2 (valores que hacen cero el coseno, y por tanto anularían el denominador). Si a(x) es un polinomio, entonces: $D o m_{f} = \{x \in ℝ / a (x) \neq (2 k + 1) \frac{π}{2} con k \in ℤ\}$ .

Funciones tangente

En la ilustración, la gráfica de la función tangente ( abreviada tan(x) ). Los múltiplos impares de π/2 no están incluidos en el dominio, como puede verse en la aparición de asíntotas verticales.

Puedes consultar un análisis detallado de las funciones trigonométricas directas en el apartado enlazado.

Función cosecante

*Expresión general*	*Ejemplos*
$f (x) = \csc (a (x))$	$f (x) = \csc (x) g (x) = \csc (3 x^{2} + 2) h (x) = \csc (- 5 x + x^{3})$

En estos casos es bueno recordar que la cosecante se define como $\csc (a (x)) = \frac{1}{\sin (a (x))}$ , con lo que impone que el valor del argumento a(x) no sea un múltiplo de π (valores que hacen cero el seno, y por tanto anularían el denominador). Si a(x) es un polinomio, entonces: $D o m_{f} = \{x \in ℝ / a (x) \neq k π con k \in ℤ\}$ .

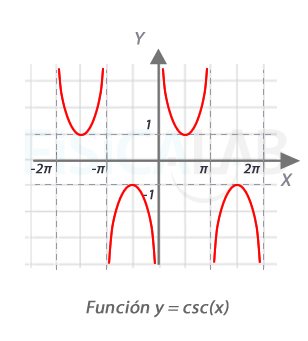
Funciones cosecante

En la ilustración, la gráfica de la función cosecante ( abreviada csc(x) ). Los múltiplos de π no están incluidos en el dominio, como puede verse en la aparición de asíntotas verticales. Por otro lado, los valores en los que la función vale 1 o -1 coinciden con los valores en los que la función seno también se hace 1 ó -1 (estos son, los múltiplos impares de π/2 ).

Función secante

*Expresión general*	*Ejemplos*
$f (x) = \sec (a (x))$	$f (x) = \sec (x) g (x) = \sec (3 x^{2} + 2) h (x) = \sec (- 5 x + x^{3})$

En estos casos es bueno recordar que la secante se define como $\sec (a (x)) = \frac{1}{\cos (a (x))}$ , con lo que impone que el valor del argumento a(x) no sea un múltiplo de π/2 (valores que hacen cero el coseno, y por tanto anularían el denominador). Si a(x) es un polinomio, entonces: $D o m_{f} = \{x \in ℝ / a (x) \neq (2 k + 1) \frac{π}{2} con k \in ℤ\}$ .

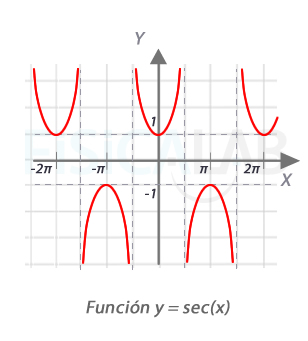
Funciones secante

En la ilustración, la gráfica de la función secante ( abreviada sec(x) ). Los múltiplos impares de π/2 no están incluidos en el dominio, como puede verse en la aparición de asíntotas verticales. Por otro lado, los valores en los que la función vale 1 o -1 coinciden con los valores en los que la función coseno también se hace 1 ó -1 (estos son, los múltiplos de π ).

Función cotangente

*Expresión general*	*Ejemplos*
$f (x) = \cot (a (x))$	$f (x) = \cot (x) g (x) = \cot (3 x^{2} + 2) h (x) = \cot (- 5 x + x^{3})$

En estos casos es bueno recordar que la cotangente se define como $\tan (a (x)) = \frac{1}{\tan (a (x))} = \frac{\cos (a (x))}{\sin (a (x))}$ , con lo que impone que el valor del argumento a(x) no sea un múltiplo de π (valores que hacen cero el seno, y por tanto anularían el denominador). Si a(x) es un polinomio, entonces: $D o m_{f} = \{x \in ℝ / a (x) \neq k π con k \in ℤ\}$ .

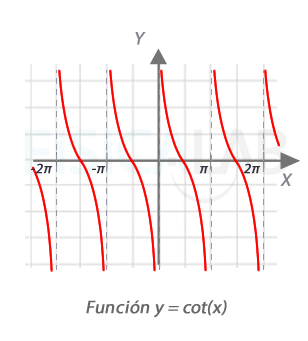
Funciones cotangente

En la ilustración, la gráfica de la función cotangente ( abreviada cot(x) ). Los múltiplos de π no están incluidos en el dominio, como puede verse en la aparición de asíntotas verticales.

Dominio a partir de operaciones con funciones

Cuando las funciones anteriores aparecen como partes de otra función, ya sea en sumas, restas, multiplicaciones o divisiones, buscamos el dominio de la función global como el conjunto de aquellos valores que cumplen a la vez todas las restricciones vistas, esto es:

$D o m_{f + g} = D o m_{f - g} = D o m_{f \cdot g} = D o m_{f} \cap D o m_{g}$
$D o m_{f / g} = D o m_{f} \cap D o m_{g} - \{x \in D o m_{g} / g (x) = 0\}$

Ten presente que para poder simplificar una función que hayas obtenido operando con otras funciones debes indicar claramente el dominio, y este debe ser el de la función original. De lo contrario podrías obtener una función después de la simplificación que no coincida con la original.

Observa el siguiente ejemplo. Partimos de las siguientes funciones: $f (x) = \frac{x - 1}{x + 1}; g (x) = \frac{x^{2} + 1}{x^{2} - 1}$ . Los dominios de f(x) y g(x) son respectivamente:

$D o m_{f} = ℝ - \{- 1\} D o m_{g} = ℝ - \{\pm 1\}$

Si formamos una función...

$(f \cdot g) (x) = \frac{x - 1}{x + 1} \cdot \frac{x^{2} + 1}{x^{2} - 1} con D o m_{f \cdot g} = D o m_{f} \cap D o m_{g} = ℝ - \{\pm 1\}$

Cuando simplifiquemos f·g debemos indicar el mismo dominio...

$(f \cdot g) (x) = \frac{x - 1}{x + 1} \cdot \frac{x^{2} + 1}{x^{2} - 1} \underset{a^{2} - b^{2} = (a + b) \cdot (a - b)}{=} \frac{(x - 1) \cdot (x^{2} + 1)}{(x + 1) \cdot (x + 1) \cdot (x - 1)} \Rightarrow (f \cdot g) (x) = \frac{x^{2} + 1}{{(x + 1)}^{2}} con D o m_{f \cdot g} = D o m_{f} \cap D o m_{g} = ℝ - \{\pm 1\}$

Y no caer en la tentación de "recalcular" este:

$(f \cdot g) (x) = \frac{x^{2} + 1}{{(x + 1)}^{2}} con D o m_{f \cdot g} = ℝ - \{- 1\}$

Función compuesta

Como veremos en detalle en un apartado dedicado, dadas dos funciones f(x) y g(x) podemos obtener otra función llamada función compuesta que transforma cada valor de x en un valor g[f(x)]. A dicha función se la llama f compuesta con g y se denota por (g ∘ f)(x).

$D o m_{g \circ f} : x \in D o m_{f} \land f (x) \in D o m_{g}$

Donde:

El símbolo ∧ representa la condición "y", es decir, la intersección de los conjuntos de valores obtenidos al aplicar cada condición

Visita el apartado señalado para profundizar en el estudio de la función compuesta, su dominio y sus propiedades.

Función definida a trozos

En ocasiones una función no está dada por una sola ecuación, sino que cambia su comportamiento según los valores de x. Una función definida a trozos es una función en la que cada tramo de valores de x o rama corresponde con una ecuación distinta.

El dominio de una función definida a trozos es la unión de los dominios de cada rama. Por ejemplo, el dominio de la función...

$f (x) = \{\begin{matrix} x & si x \leq - 3 \\ \frac{1}{x} & si - 2 \leq x < 5 \\ x^{2} + 1 & si x \geq 5 \end{matrix}$

... viene dado por la unión de los dominios de cada una de las ramas, teniendo en cuenta los intervalos de valores que la definen: $D o m_{f} = D o m_{1} \cup D o m_{2} \cup D o m_{3}$ .

$D o m_{1} = (- \infty, - 3]$ : Observa como aunque esta rama sea un polinomio, cuyo dominio sería $ℝ$ , solamente nos quedamos con los valores incluidos en la rama (hasta -3)
$D o m_{2} = [- 2, 5) - {0}$ , que también podríamos expresar: $D o m_{2} = [- 2, 0) \cup (0, 5)$
$D o m_{3} = [5, \infty)$ : También es un polinomio, y volvemos a escoger solamente los valores incluidos en la rama

Finalmente, el dominio de la función es la unión de los 3 conjuntos anteriores:

$D o m_{f} = (- \infty, - 3] \cup [- 2, 0) \cup (0, 5) \cup [5, \infty) = (- \infty, - 3] \cup [- 2, \infty) - \{0\}$

Funciones definidas gráficamente

Si encuentras una función expresada gráficamente puedes calcular su dominio proyectándola sobre el eje de abscisas ( eje x ). Para ello puedes imaginar que iluminas con una luz desde la propia función hacia el eje x. La zona iluminada del eje corresponde a los valores incluidos en el dominio. Recuerda que la búsqueda del dominio consiste en buscar los puntos de x que tienen imagen. Las siguientes convenciones en la representación gráfica de funciones son útiles para el cálculo del dominio:

Un punto sólido en la gráfica de la función indica que el mismo forma parte de la gráfica
Un punto transparente en la gráfica de la función indica que el mismo no forma parte de la gráfica
Una línea vertical punteada a la que se aproxima la función, sin tocarla, por su lado izquierdo, por su lado derecho, o por ambos, representa una asíntota vertical. El valor de x de la asíntota no es alcanzado por la función
Si el extremo de una gráfica, derecho o izquierdo, no incluye ningún punto como los anteriores, se supone que la gráfica continuaría con la misma tendencia en ese extremo

Ejemplo:

Dominio de una función definida graficamente

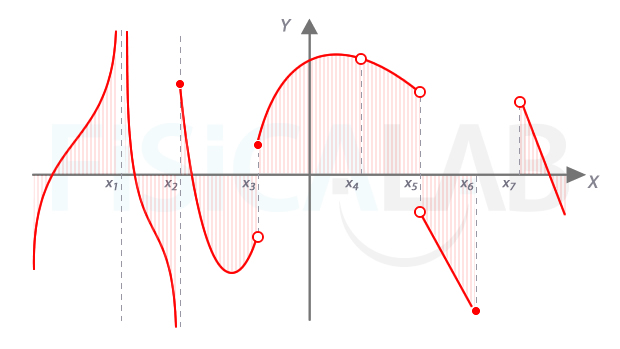
Dominio a partir de gráfica

En la ilustración aparece, en rojo, una función definida gráficamente con distintas ramas. Para calcular el dominio, primeramente proyectamos sobre el eje x la función. Las áreas rayadas corresponden a dicha proyección. Los puntos que pueden presentar dudas se han marcado sobre el eje x desde x₁ a x₇.

A partir de la gráfica anterior repasamos, de izquierda a derecha, los valores del eje x para determinar el dominio. Podemos considerar cada área rayada, y posteriormente simplificar el conjunto obtenido, quedándonos:

$D o m_{f} = (- \infty, x_{1}) \cup (x_{1}, x_{2}) \cup [x_{2}, x_{3}) \cup [x_{3}, x_{4}) \cup (x_{4}, x_{5}) \cup (x_{5}, x_{6}] \cup (x_{7}, \infty) = = (- \infty, x_{6}) \cup (x_{7}, \infty) - \{x_{1}, x_{4,} x_{5}\}$

Veamos en detalle el proceso que hemos seguido, una vez proyectada la función sobre el eje x :

En primer lugar tenemos que determinar el extremo inferior del dominio. Dado que el extremo izquierdo de la gráfica no presenta ningún punto sólido, debemos suponer que continua con esa tendencia hasta -∞. Ese será el extremo inferior.
La proyección continúa hasta x₁ . La gráfica se aproxima a dicho valor de x sin llegar a tocarlo, tanto por la izquierda como por la derecha. Además, está marcado por una linea discontinua que se "pierde" por los márgenes superior e inferior de la ilustración: se trata de una asíntota vertical. Como tal, el valor x₁ no debe estar incluido en el dominio
Algo similar ocurre con x₂ por su lateral izquierdo, sin embargo la rama a la derecha indica explícitamente que dicho valor si está en la gráfica. Por tanto x₂ sí está en el dominio
La proyección continúa sin problema hasta x₃, donde nos encontramos que no está contenido por la rama más a la izquierda, al estar marcado con un punto transparente. Sin embargo el valor si que está incluido por la rama más a la derecha. Por tanto x₃ si está incluido en el dominio
El siguiente valor que llama nuestra atención es x₄. Dicho valor no está incluido en el dominio (punto transparente)
Continuamos hasta x₅. Valor que no está incluido en la gráfica ya que ni por la rama más a la izquierda ni por la de la derecha hay ningún punto sólido
Continuaríamos hasta x₆, cuyo punto sólido nos indica que se encuentra en el dominio
Nos encontramos ahora con un salto, hasta x₇, valor no incluido en el dominio
Finalmente, el extremo superior del dominio vendría marcado por ∞, ya que la última rama, una recta, continuaría con la misma tendencia decreciente por siempre

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.