Funciones Logarítmicas

Las escalas utilizadas para medir fenómenos físicos que crecen muy rápidamente suelen ser logarítmicas. Por ejemplo, la escala de Ritcher, utilizada para medir la intensidad de los terremotos, o las escalas de intensidades sonoras, medidas en decibelios (dB). Para poder estudiarlas bien, debes conocer las funciones logarítmicas y sus propiedades, en las que vamos a profundizar a través de los siguientes epígrafes:

• Definición
• Gráficas
• Dominio
• Recorrido o imagen
• Continuidad y derivabilidad
• Monotonía, máximos y mínimos
• Curvatura
• Cortes con los ejes x e y y cambios de signo
• Asíntotas y ramas
• Simetría
• Representación
• Aplicaciones prácticas

Para ayudarte a visualizar todas estas propiedades te aconsejamos que te ayudes de este simulador de funciones logarítmicas. ¿Preparado para aumentar los decibelios de tu conocimiento?

Definición

Ejemplos

$$\begin{array}{cc}\mathit{a}\mathbf{)} f\left(x\right)=lo{g}_3\left(x\right)& \mathit{b}\mathbf{)} \mathrm{f}\left(\mathrm{x}\right)={\log }_{1/2}\left(\mathrm{x}\right)\\ \mathit{c}\mathbf{)}\mathbf{ }\mathrm{f}\left(\mathrm{x}\right)={\log }_{10}\left(\mathrm{x}\right)& \mathit{d}\mathbf{)} \mathrm{f}\left(\mathrm{x}\right)={\log }_e\left(\mathrm{x}\right)\\ \mathit{e}\mathbf{)} \mathrm{f}\left(\mathrm{x}\right)={\log }_{2/5}(1+\mathrm{x})-2& \mathit{f}\mathbf{)}\mathbf{ }\mathrm{f}\left(\mathrm{x}\right)=3·{\log }_2\left(\mathrm{x}\right)\end{array}$$

Observa:

• Las funciones en a), b), c) y en d) son funciones logarítmicas sencillas, en la forma expresada en la definición, crecientes o decrecientes según el valor de la base
• Las funciones en e) y en f) son funciones logarítmicas en las que se ha aplicado alguna transformación
• La función en c) es un logaritmo de base 10. A estos logaritmos se les conoce como logaritmos decimales, y se pueden expresar f(x)=log₁₀(x)=log(x)
• La función en d) es un logaritmo de base el número de Euler e. A estos logaritmos se les conoce como logaritmos neperianos o naturales, y se pueden expresar f(x)=log_e(x)=ln(x)

Gráficas

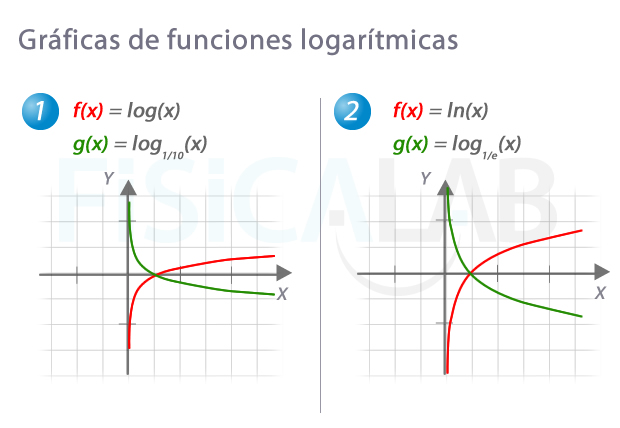
Funciones logarítmicas

Las gráficas en rojo corresponden a las dos funciones logarítmicas más utilizadas, ambas de base mayor que 1. Por otro lado, las funciones en verde corresponden a dos logarítmicas de base menor que 1. Observa como en las funciones logarítmicas, pequeños cambios en x provocan grandes cambios en y cuando x<1. Luego, para valores de x>1 los cambios en y son muy pequeños.

Finalmente, dado que cualquier número distinto de 0 elevado a 0 es 1, las cuatro funciones pasan por (1,0), y dado que a¹=a, todas pasan por (a,1).

Como vimos, también podemos encontrar funciones logarítmicas un poco más complejas.

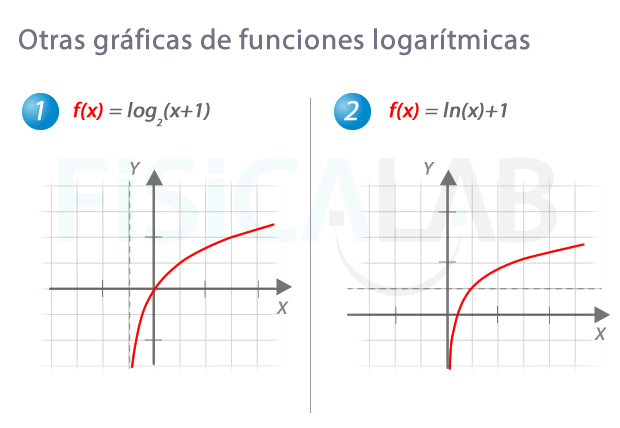
Funciones logarítmicas más complejas

La gráfica en 1 se puede obtener a partir de la de f(x)=log₂(x), desplazándola una unidad a la izquierda. Por otro lado, la función en 2 la hemos obtenido desplazando una unidad hacia arriba la función f(x)=ln(x).

Como ves, en todos estos casos, las funciones logarítmicas son inyectivas, pues no existen dos valores de y iguales para la misma x.

Dominio

Dado que es imposible obtener un número negativo elevando un número positivo (la base) a cualquier otro, no es posible hablar de logaritmos de números negativos. Por otro lado, dado que no es posible obtener 0 como resultado de elevar un número positivo (la base) a otro, tampoco podemos hablar del logaritmo de 0.

En el caso de funciones más complejas de tipo f(x)=log_a(g(x)) asegúrate de hacer g(x)>0. Asegúrate de sustraer del dominio de f(x) también los elementos que no estén en el dominio de g(x).

Revisa el apartado sobre cálculo de dominio de cualquier función para instrucciones más detalladas sobre el cálculo del mismo.

Recorrido

El recorrido de la función logarítmica tipo f(x)=log_a(x), es el conjunto de los reales: Rec_f=ℝ.

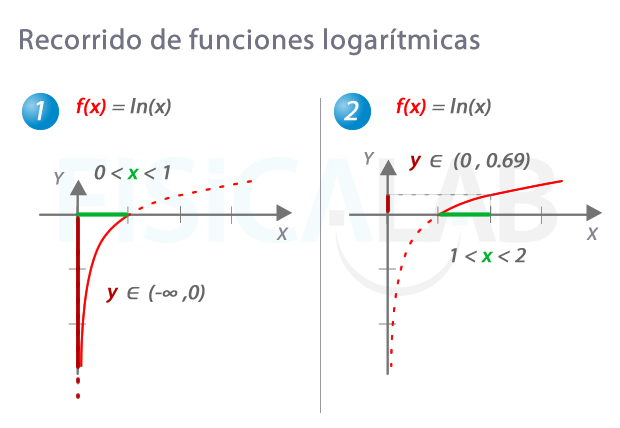
Comportamiento de las imágenes de funciones logarítmicas

Según el rango de valores de la variable independiente, la variable dependiente se comporta de muy distinta manera. Observa, en 1, que las imágenes de la función se incrementan desde -∞ hasta 0, en un incremento de x de tan solo una unidad. Por el contrario, para valores de x a partir de 1 el crecimiento "se comprime". Así, en 2, la variable dependiente se incrementa en tan solo 0.69 unidades para un incremento de la variable independiente igual a 1. Es por esto que las funciones logarítmicas se suelen utilizar para "comprimir" el rango de funciones cuando es necesario, como por ejemplo cuando usamos los decibelios (dB).

Para profundizar en el estudio del recorrido de funciones cualesquiera visita el apartado enlazado.

Continuidad y derivabilidad

Crecimiento, decrecimiento y extremos

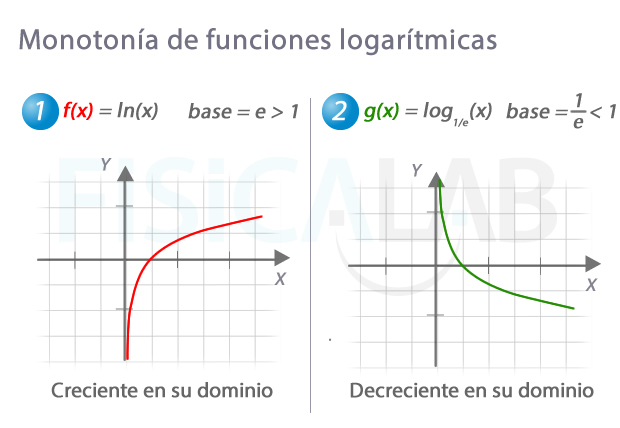
Monotonía en funciones logarítmicas

Como ves, si la base es mayor que 1, caso de la imagen izquierda, a medida que tomamos valores mayores de la abscisa x los valores de la ordenada y se van haciendo más grandes también. Por eso es creciente. En caso de que la base esté en el intervalo (0,1) (imagen derecha) a medida que tomamos valores mayores de la abscisa x los valores de en el eje y se van haciendo más pequeños. Por eso es decreciente.

Para funciones logarítmicas más complejas te recomendamos que sigas los pasos habituales para el estudio de la monotonía.

Curvatura y puntos de inflexión

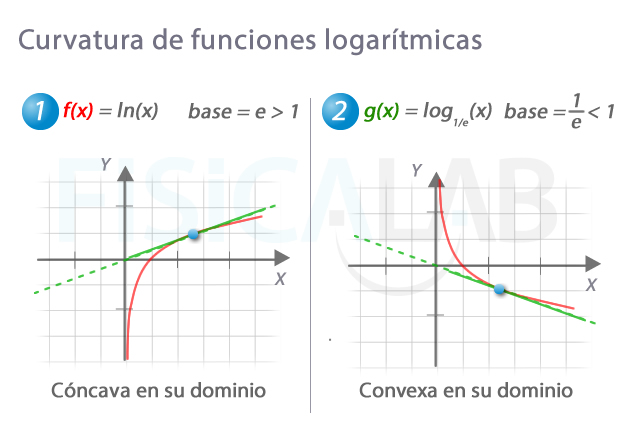
Curvatura en funciones logarítmicas

A la izquierda, una función logarítmica de base mayor que 1. Como ves, la recta tangente en cualquier punto, representada en verde, siempre queda por encima de la función. Por eso es cóncava en todo su dominio. A la derecha, una función logarítmica con base menor que 1. La recta tangente, en este caso, queda siempre por debajo de la función. Por eso es convexa en todo su dominio.

Para funciones logarítmicas más complejas te recomendamos que sigas los pasos habituales para el estudio de la curvatura.

Cortes con los ejes y cambio de signo

Corte con eje x

El procedimiento habitual consiste en hacer f(x)=0 y despejar la variable independiente x. En el caso de las funciones tipo f(x)=log_a(x), esto ocurre cuando x=1, ya que log_a(1)=0. En el caso de funciones un poco más complejas, tipo f(x)=log_a(g(x)) habría que buscar los valores de x tales que g(x)=1, que es lo mismo que g(x)-1=0. Si no existiesen no habría corte con eje x, como sucede por ejemplo con f(x)=ln(x²+2).

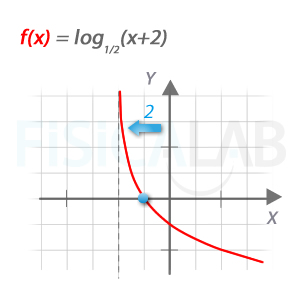
Corte con eje x

Observa la función de la gráfica. Haciendo 0=log_1/2(x+2)⇒x+2=1⇒x=-1 obtenemos el punto de corte con el eje x.

Otra forma de pensar en el problema es partir de la función g(x)=log_1/2(x) y desplazarla dos unidades hacia la izquierda f(x)=g(x+2).

Corte con eje y

En este caso el procedimiento general consiste en hacer x=0 y resolver. La función tipo f(x)=log_a(x) no presenta corte con el eje y, al no poder resolver y=log_a(x). No obstante, en funciones un poco más complejas sí que puede aparecer dicho corte.

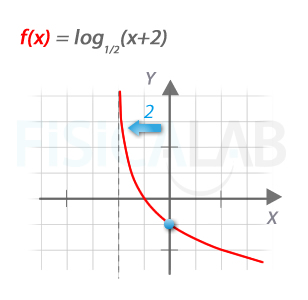
Corte con eje y

En la función de la gráfica, si hacemos x=0 obtenemos el punto de corte con el eje y resolviendo y=log_1/2(0+2)=-1.

Otra forma de pensar en el problema es partir de la función g(x)=log_1/2(x) y desplazarla dos unidades hacia la izquierda f(x)=g(x+2).

Cambio de signo

Las funciones logarítmicas tipo f(x)=log_a(x) tienen un cambio de signo en x=1.

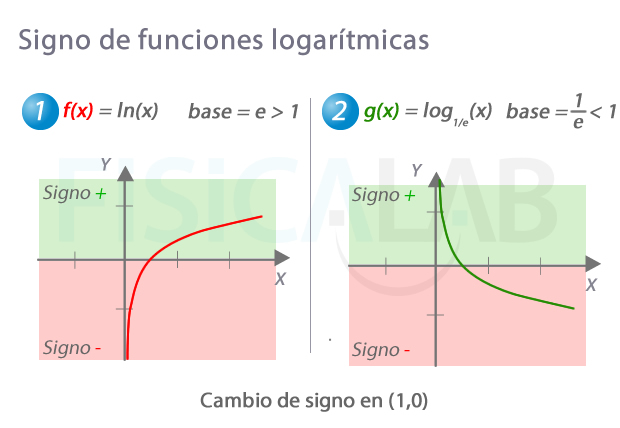
Signo de gunciones logarítmicas tipo

Para cualquier función logarítmo de x, si la base es mayor que 1 el punto en el que la función cambia de negativa a positiva es el (1,0). En el caso de que la base sea menor que 1, en este punto la función pasa de positiva a negativa.

Asíntotas y ramas

Las funciones logarítmicas sencillas tipo f(x)=ln_a(x) tienen 2 tipos de ramas infinitas: 1 rama parabólica y una asíntota vertical.

• Rama parabólica: Se da cuando:

  $$\underset{x\to \infty }{\lim }f\left(x\right)=\pm \infty$$

• Asíntota vertical: Se da cuando:

  $$\underset{x\to 0^{+}}{\lim }f\left(x\right)=\pm \infty$$

  Siendo en este caso x=0 la asíntota vertical

Ramas infinitas en logarítmicas

En la imagen superior puedes encontrar las ramas infinitas que aparecen en una función logarítmica tipo en función del valor de su base.

Si deseas estudiar el cálculo de ramas infinitas en funciones logarítmicas más complejas, visita los apartados enlazados.

Simetría

Como hemos podido ver en el epígrafe de "gráficas", las funciones logarítmicas tipo f(x)=log_a(x) no presentan simetría par ni impar. No obstante, sí que puedes encontrar funciones en las que aparezcan logaritmos que sean simétricas a través, por ejemplo, de la composición de funciones.

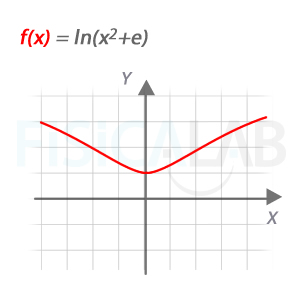
Una función simétrica

La función de la gráfica presenta simetría par. Se puede entender como la composición f(x)=(g∘h)(x)=g[f(x)] con g(x)=log(x) y h(x)=x²+e.

Por otro lado, podemos encontrar simetrías:

• Entre f(x)=log_a(x) y f(x)=log_1/a(x) respecto al eje x
• Entre la función exponencial f(x)=a^x y la logarítmica f(x)=log_a(x) respecto a la recta y=x

Representación

A partir de la forma general que hemos estudiado en el epígrafe de gráficas, es inmediato esbozar funciones logarítmicas sencillas:

• Sabemos que pasan por el punto (1,0) y (a, 1)
• Serán crecientes si la base es mayor que uno y decrecientes si la base está entre 0 y 1
• Si necesitamos más precisión, construimos una tabla de valores

Si la función a representar es compleja, como por ejemplo $f\left(x\right)=\log \left(\frac{x^2}{x+2}\right)$, te recomendamos que sigas los pasos genéricos para representación gráfica de funciones.

Aplicaciones

Las funciones logarítmicas se utilizan principalmente en la descripción de fenómenos que tienen que ver con la percepción.

• Leyes Weber-Fechner: También conocida como ley psicofísica, relaciona la sensación percibida con la intensidad de un estímulo físico. Estos estímulos físicos pueden ser de muy diferente tipo: sonidos, iluminación, sabor...

  

  Ley psicofísica

  Cuando tenemos un sonido de poca intensidad, por ejemplo, un individuo puede ser capaz de percibir cambios pequeños en el mismo. Esos cambios se pueden medir como variaciones de una magnitud física (la intensidad sonora). Sin embargo, cuando la intensidad del sonido es grande, pequeñas variaciones en la magnitud física pasan desapercibidas para el individuo.

  Otro ejemplo práctico. Imagina un grupo de 2 pájaros volando juntos en el cielo. Si ahora un nuevo pájaro se uniera a ellos, probablemente no tendrías problema alguno en distinguirlo. Sin embargo, si el grupo inicial de pájaros fuera de 12, te costaría trabajo distinguir cuando se ha unido uno nuevo dando lugar a 13

• Decibelios (dB): Se trata de una unidad adimensional que nos permite la comparación de dos cantidades de presión sonora, tensión ó potencia eléctrica entre otras. Nos permite representar grandes cantidades a través de números pequeños

  

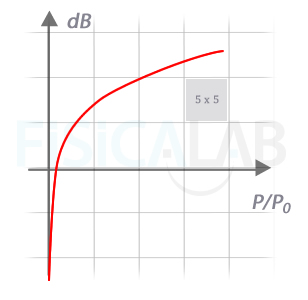
  Decibelios de potencia

  Para la potencia eléctrica podemos definir el decibelio según $dB=10·{\log }_{10}\left(\frac{P}{P_0}\right)$, siendo P₀ una potencia de referencia y P la potencia a comparar. Así, un aumento del doble de potencia correspondería a un incremento aproximado de 3dB.

  Visita el apartado asociado para profundizar sobre ello.