Funciones Reales de Variable Real

Una función es una relación entre dos conjuntos en la que a cada valor del primer conjunto, denominado dominio, le corresponde un único valor del segundo conjunto, denominado recorrido. Decimos que estamos ante una función real de variable real cuando tanto el primer conjunto como el segundo está formados por números reales. En este apartado vamos a estudiar dichas funciones a través de los siguientes puntos:

Definición
- Restricciones del dominio
- Ejemplos de funciones reales
Representación gráfica
- La prueba de la recta vertical
Aplicaciones en física
Conclusión

¿Empezamos?

Definición

Se define una función real de variable real, o simplemente función real, como aquella función matemática que hace corresponder a cada número real $x \in ℝ$ otro número real $y \in ℝ$ a través de una regla de transformación f(x). Formalmente:

$\begin{matrix} f : & D o m_{f} & \to & ℝ \\ x & \mapsto & y = f (x) \end{matrix}$

Donde:

f : Es la función de ℝ en ℝ, es decir, una regla de correspondencia que asigna a cada valor ℝ del dominio otro número real
Dom_f : Es el dominio de definición de la función f, también llamado campo de existencia. Esto es, el conjunto de posibles valores que puede tomar la entrada de la función, es decir, que tienen imagen. Puede ser, o bien el conjunto completo de los reales ( ℝ ), o bien un subconjunto de este: $D o m_{f} \subseteq ℝ$ . Más formalmente: $D o m_{f} = \{x \in ℝ / \exists y = f (x) \in ℝ\}$
ℝ : Es el codominio de la función, es decir, el conjunto de posibles valores que podría tomar la variable dependiente
x : Es la variable independiente. En este caso, un número real que hace las veces de entrada de la función
y=f(x) : Es la variable dependiente, imagen de x. Es un número real que hace las veces de salida. Para obtener su valor se aplica la función sobre el elemento x

Recuerda el significado de los siguientes símbolos:

∃ existe un
∀ para todo
∈ pertenece a
/ tal que
⊂ subconjunto de
⊆ subconjunto o igual a

Ten presente que, aunque no esté en la definición, el recorrido es igualmente importante. Es llamado también conjunto imagen o simplemente imagen de la función, y es el conjunto de valores que realmente toma la salida. Formalmente, $R e c_{f} = \{y \in ℝ / \exists x \in D o m_{f} con f (x) = y\}$

Es un error muy habitual confundir el recorrido con el codominio. Recuerda que este último es el conjunto de valores que podría tomar la salida. En las funciones reales de variable real tanto el dominio, como el codominio, como el conjunto imagen son números reales ( $D o m_{f} \subseteq ℝ$ , $C o d_{f} \subseteq ℝ$ , $R e c_{f} \subseteq ℝ$ ). Visita el apartado de funciones matemáticas si necesitas aclarar estas ideas.

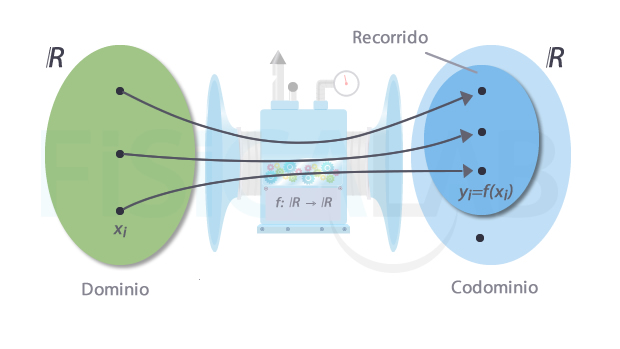
Función real

En la ilustración representamos el concepto de función real de variable real. Observa que la función f es una correspondencia, representada en la ilustración por una máquina azul, que asocia a cada elemento de un conjunto inicial llamado dominio (formado por números reales), otro número real de un conjunto denominado imagen o recorrido. Decimos que cada elemento concreto y_i del recorrido es la imagen de un determinado elemento x_i del dominio según y_i=f(x_i) . Decimos que x_i es su antiimagen.

Restricciones del dominio

En ocasiones puede resultar útil restringir el dominio de una función real a un subconjunto de ℝ. Recuerda que, aunque no se suela dar de manera explícita, tanto el dominio como el codominio forman parte de la propia definición formal de una función, y pueden cambiar enteramente las propiedades de esta, o incluso hacer que una correspondencia deje de ser considerada una función. De manera general, restringiremos el dominio de una función:

Cuando sea matemáticamente imposible realizar alguna operación con ciertos valores x
Cuando el contexto real del que se ha obtenido la función así lo determine
Cuando lo necesitemos por alguna otra razón

Dedicaremos un apartado a aprender a calcular el dominio de una función real cuando no nos lo den de manera explícita. De momento, los siguientes ejemplos de funciones reales te ayudarán a entender mejor los casos señalados.

Ejemplos

Las siguientes funciones están expresadas mediante una ecuación algebraica. En todos los casos hemos prescindido de la definición formal del dominio y del codominio. Observa:

$f (x) = \frac{3}{2} x + 2$

La función f es una función lineal (se trata de un polinomio de orden 1). Su dominio, si así lo decido en su definición, podría estar formado por todos los números reales, pues todos ellos tienen una imagen. Así, la imagen de x=2 es $y = f (2) = \frac{3}{2} 2 + 2 = 5$ . De igual manera, el codominio, si así lo decidiese en su definición, también podría estar formado por todo ℝ.
$g (x) = \frac{1}{x}$

En esta ocasión, la función g es una función de proporcionalidad inversa. Dado que resulta imposible matemáticamente dividir entre 0, debemos "quitarlo" del dominio. Nuestro dominio de definición podría ser en este caso: Dom_f=ℝ-{0}=(-∞,0)∪(0,∞).
$s (t) = \frac{1}{2} \cdot 3 \cdot t^{2}$

La función s tiene como variable independiente t. Observa que se trata de la ecuación del espacio que recorre un cuerpo sometido a una aceleración constante, en la que t representa el tiempo. En este contexto, podría tener sentido restringir el dominio de dicha función a los valores de t positivos, quedando Dom_s=[0,∞).
$g (x) = x^{2}$

La función g es una función cuadrática (polinomio de orden 2). Como tal, podríamos decidir que su dominio es el conjunto de los números reales. Observa que también podríamos decidir que, al igual que hicimos con la función s, su dominio fuesen solo los reales positivos. De esta manera, según hagamos una elección u otra, las propiedades de g cambian: Si elegimos todos los reales como dominio, dos elementos distintos del dominio podrían tener igual imagen ( g(-1)=g(1)=1 ); en cambio, si sólo elegimos los reales mayores que cero, cada elemento del dominio tendrá una imagen distinta. Como puedes ver, el dominio es una parte muy importante en la definición de una función.
$h (x) = \sqrt{x}$

La función h es una función raíz. Un momento... ¿estás seguro que la raíz cuadrada es una función? Si lo piensas un poco, dos elementos distintos del dominio podrían tener la misma imagen ( $f (4) = \sqrt{4} = \pm 2$ , por ejemplo ) y habíamos dicho que las funciones deben ser univaluadas, es decir, que a cada elemento del dominio le corresponderá un único elemento del conjunto final. Para que la función raíz sea una función, debemos restringir el codominio, por ejemplo, a los reales positivos, o a los reales negativos. Como puedes ver, el codominio también es una parte muy importante en la definición de una función. No obstante en este nivel, y dado que ya hemos dicho que no es habitual encontrar el dominio y el codominio definidos de manera explícita, nos guiaremos por la siguiente convención:
- $h (x) = \sqrt{x} \Rightarrow C o d_{f} = [0, \infty)$
- $h (x) = - \sqrt{x} \Rightarrow C o d_{f} = (- \infty, 0]$

Aunque menos habitual en este nivel educativo, también es posible que encuentres una función expresada de manera implícita, esto es, sin despejar la variable dependiente. Por ejemplo: $x^{2} - y = 0$

Representación gráfica

Una función real de variable real está constituida por pares ordenados de elementos de ℝ, en la forma (x,f(x)). Dichos pares pueden ser representados sobre un sistema de ejes cartesianos mediante puntos P(x,y), con y=f(x). Sigue los siguientes pasos:

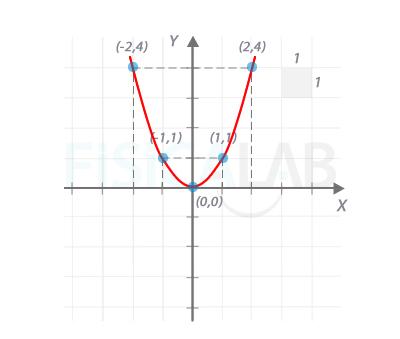
Elige el intervalo de valores del dominio que vas a representar. Por ejemplo, vamos a representar el intervalo [-2, 2] de la función f(x)=x²
Decide el número de puntos que vas a representar. Por ejemplo, cinco puntos. Recuerda que en el dominio de los números reales, la cantidad de puntos que podrías representar es ilimitada, así que cuantos más puntos decidas representar, más precisa será la representación

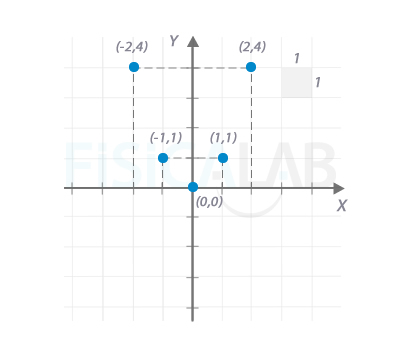
Elabora una tabla de valores con los puntos que vas a representar. La coordenada x de cada punto, debe pertenecer al dominio. Los puntos estarán situados de manera equiespaciada. La coordenada y de cada punto se obtiene como la imagen de los valores de x anteriores, aplicando la definición de la propia función. En nuestro caso, dado que hemos elegido 5 puntos, nos quedará x₁=-2, x₂=-1, x₃=0, x₄=1, x₅=2 , y la tabla nos queda:

x	y
x₁=-2	y₁=f(x₁)=f(-2)=(-2)²=4
x₂=-1	y₂=f(x₂)=f(-1)=(-1)²=1
x₃=0	y₃=f(x₃)=f(0)=0²=0
x₄=1	y₄=f(x₄)=f(1)=1²=1
x₅=2	y₅=f(x₅)=f(2)=2²=4

Pinta un sistema de coordenadas cartesianas x-y (eje de abscisas-eje de ordenadas).

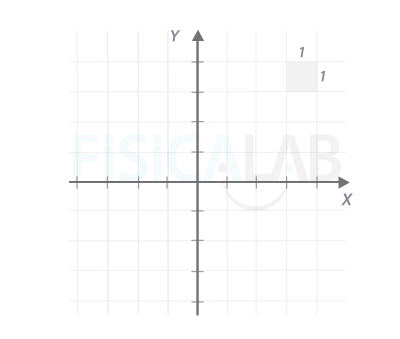
Ejes cartesianos

Ejes cartesianos. El eje horizontal es el eje x, y también se llama eje de abscisas. El eje vertical es el eje y, y también se llama eje de ordenadas. Cada subdivisión de los ejes representa una unidad, tal y como se ilustra en el cuadro gris.
Pinta cada punto sobre el sistema de coordenadas anterior
Une los puntos y obtén la representación final

En la ilustración siguiente representamos algunas otras funciones:

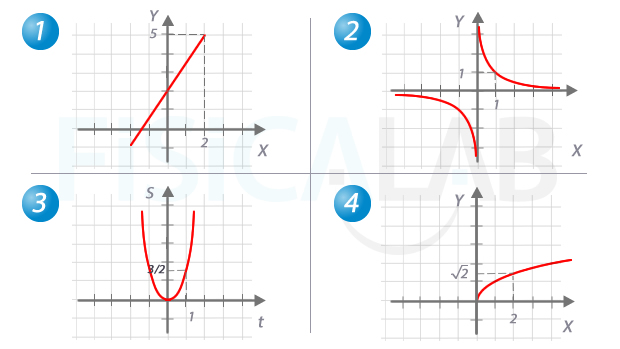
Gráficas de funciones

En la ilustración superior tenemos representadas 4 funciones distintas. La primera es una función linea, concretamente $f (x) = \frac{3}{2} x + 2$ . La segunda es una función de proporcionalidad inversa, concretamente $g (x) = \frac{1}{x}$ . La tercera es una función cuadrática en la que la variable independiente se llama t y la variable dependiente s $s (t) = \frac{1}{2} \cdot 3 \cdot t^{2}$ . Finalmente la cuarta es la función raíz cuadrada positiva $h (x) = \sqrt{x}$ . En todas ellas hemos marcado, sobre el eje horizontal, algún valor del dominio. Observa como, a través de la gráfica, obtenemos las imágenes correspondientes.

Experimenta y Aprende

Cargando...

Calculadora gráfica de funciones

Ayúdate de esta potente calculadora gráfica para trazar y analizar funciones. Pulsa sobre Iniciar para comenzar a experimentar.

En niveles más avanzados estudiaremos algunas funciones tipo y nos ayudaremos de simuladores para estudiar en detalle sus gráficas y características.

La prueba de la recta vertical

En una función real, a cada elemento del dominio le corresponde un único elemento imagen. De esta manera, a cada par (x,y) le corresponde en el plano un único punto P(x,y) = P(x,f(x)). Esto se traduce en que la gráfica de una función nunca vuelve "hacia atrás". Por tanto:

En una gráfica de una función y=f(x) ninguna recta vertical la debe cortar en más de un punto.

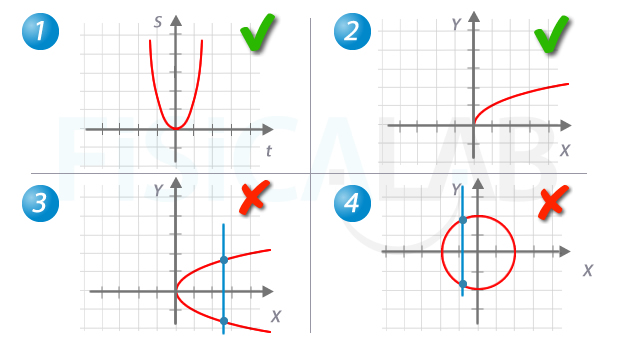
Prueba de la recta vertical

Un criterio para saber si una gráfica corresponde a una función es buscar una línea totalmente vertical que la atraviese en más de un punto. Si puedes encontrarla, significaría que para ese valor de x corresponderían varios valores de y, y por tanto la gráfica no corresponde a una función. Las gráficas 1 y 2 corresponden a funciones. La 3 y la 4 no, pues son atravesadas por las rectas verticales, en azul, en dos puntos distintos cada una.

Aplicaciones en física

Las funciones nos sirven para describir fenómenos reales. La física está llena de relaciones entre magnitudes que pueden ser estudiadas como funciones reales.

Así, por ejemplo, la energía cinética de un cuerpo viene dada por la ecuación $E_{c} = \frac{1}{2} \cdot m \cdot v^{2}$ . Si nos interesase estudiar la evolución con la velocidad de la energía cinética de un cuerpo, consideramos la velocidad la variable independiente, y fijaríamos la masa: $E_{c} (v) = \frac{1}{2} \cdot m \cdot v^{2}$ . De otro lado, si nos interesase estudiar la energía cinética que tendrían distintos cuerpos a una determinada velocidad, consideraríamos la masa la variable independiente, y fijaríamos la velocidad: $E_{c} (m) = \frac{1}{2} \cdot m \cdot v^{2}$ .

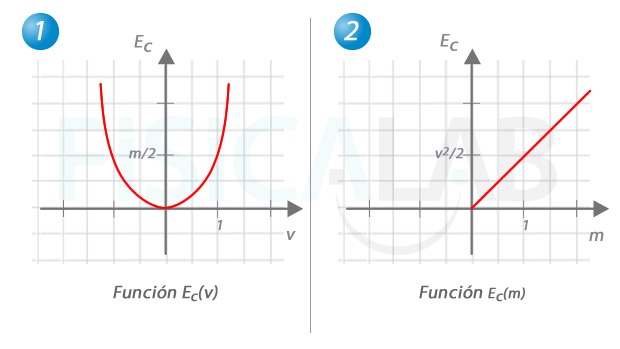
La energía cinética como función real

A la izquierda, evolución de la energía cinética con la velocidad de un cuerpo. Observa que el valor de la misma no varía tanto si la velocidad es negativa (el cuerpo se mueve hacia la izquierda) como positiva (el cuerpo se mueve hacia la derecha). A la derecha, evolución de la energía cinética según la masa del cuerpo, supuesto que la velocidad permanece constante. Observa que hemos restringido el dominio a los reales positivos, ya que no tiene sentido hablar de masas negativas.

Algunos otros ejemplos:

...y un largo etcétera que podrás estudiar a medida que profundices en los contenidos de la web.

Conclusión

Las funciones describen fenómenos concretos, de distinto tipo: físicos, químicos, económicos o incluso psicológicos. Observamos la realidad mediante la experimentación y luego buscamos los modelos generales que describan dichos fenómenos. No en vano, el concepto de función surgió históricamente en un intento de generalizar las fórmulas concretas que relacionaban las magnitudes, de igual manera que en dichas fórmulas se había pasado de utilizar números concretos a letras (variables) que representaban números cualesquiera.

En este apartado hemos estudiado las funciones reales. Gracias a ellas podemos describir distintos fenómenos que estudiaremos con profundidad en los temas de física.

A lo largo del resto del tema, utilizaremos la palabra función para referirnos exclusivamente a funciones reales de variable real.

Si has llegado hasta aquí, y has comprendido qué es una función, ya estás en disposición de visitar el resto de apartados del tema, dónde profundizaremos en la forma de calcular el dominio, los distintos tipos de funciones que hay, sus características, etc.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.