Ejercicios Resueltos de Funciones Elementales
Pon a prueba lo que has aprendido en el tema Funciones Elementales con esta lista de ejercicios con sus respectivas soluciones. Consulta:
- Ejercicios resueltos de...
- Función Matemática
- Funciones Reales de Variable Real
- Dominio de una Función
- Recorrido de una Función
- Análisis de Funciones
- Función Definida a Trozos
- Valor Absoluto de una Función
- Transformación de Funciones
- Suma y Resta de Funciones
- Multiplicación de Funciones
- División de funciones
- Función Compuesta
- Función Inversa
Ejercicios
Función Matemática
Regla de transformación en función
A partir de los diagramas de la figura, determina la regla de correspondencia o transformación, el dominio, el codominio y la imagen en cada caso.
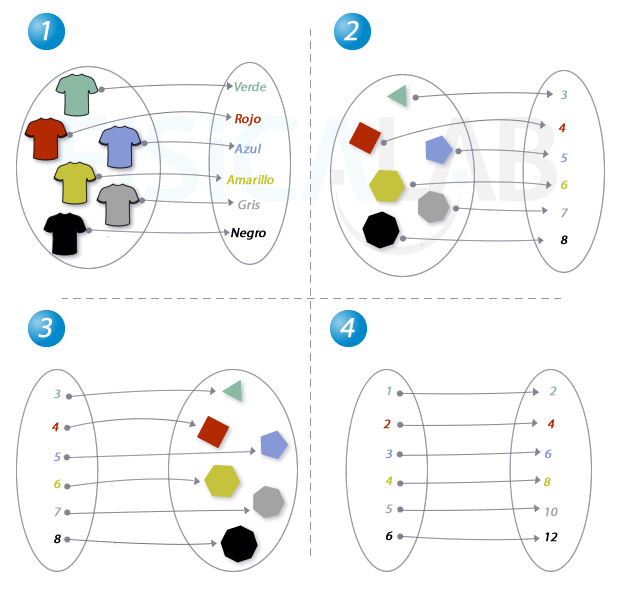
¿Es función?
En las siguientes gráficas, determina si las relaciones entre variables podrían corresponder a lo que se conoce matemáticamente como función:
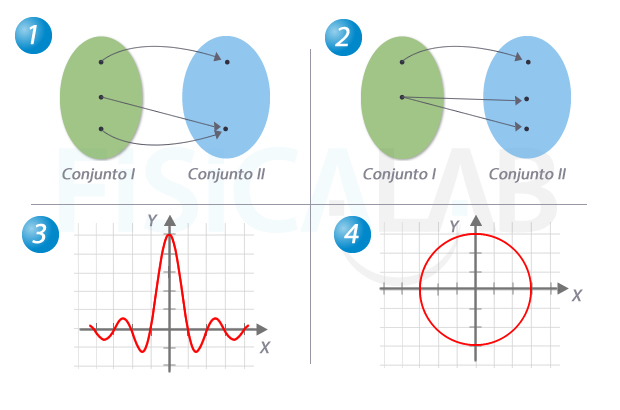
Por otro lado, haz lo mismo con las siguientes tablas:
Tabla 1
| x | 1 | 2 | 2 | 3 | 4 |
| y | 3 | 6 | 12 | 9 | 12 |
Tabla 2
| x | 0 | 0 | 1 | 2 | 0 | 2 |
| y | 0 | 1 | 0 | 0 | 2 | 1 |
| z | 0 | 1 | 1 | 2 | 2 | 3 |
Definición de función a partir de tabla
La siguiente tabla contiene pares ordenados de números naturales que han sido tomados evaluando una función de ℕ en ℕ. Define dicha función matemática y calcula f(21).
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(n) | 4 | 7 | 10 | 13 | 16 | 19 | 22 |
Funciones Reales de Variable Real
Representación gráfica con tablas de pares ordenados
Realiza un esbozo aproximado de las siguientes funciones:
Imágenes a partir de gráfica de función
Calcula la imagen de los siguientes valores de x a la luz de la siguiente gráfica: x1=-25, x2=-20, x3=-15, x4=-10, x5=-5, x6=0, x7=5, x8=10, x9=15, x10=20.
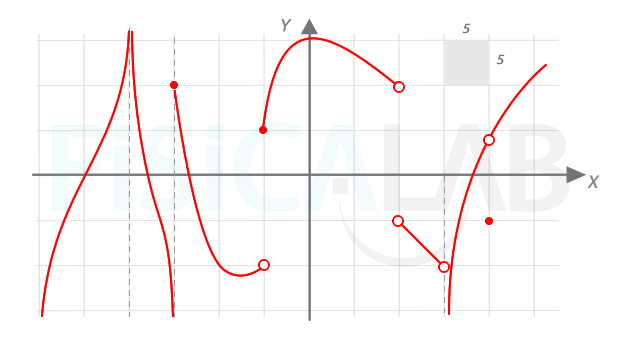
Modelar situaciones reales con funciones
Modela las siguientes situaciones mediante funciones:
- La población de una pequeña ciudad aumenta un 15% cada año. Consideramos instante inicial el año 1983 en el que la población era de 500 habitantes. ¿Cuál será la población en el año 2050, de continuar la misma tendencia?
- La temperatura media en una comarca depende de la altura, de manera que se ha observado que se reduce 1.3 ºC por cada 160 m de ascenso . Sabiendo que el punto más bajo de la comarca está al nivel del mar, y que la temperatura media allí es de 22º, ¿qué altura habrá en su lugar más alto, a 950 m?
- El coste de una llamada al extranjero tiene un precio de conexión de 0.55 €. Durante el primer minuto el contador se mantiene estático, pero una vez transcurrido este, el coste de la llamada aumenta a razón de 0.50 € cada minuto. ¿Cuál será el coste de una llamada de 20 minutos?
- Determina una función para el cálculo del radio de cilindros tomando la altura como variable independiente y sabiendo que el volumen del mismo es siempre de 314 cm3.
- Un triángulo isósceles está inscrito en una circunferencia de radio 10 cm. Halla el área del triángulo en función de su base.
Dominio de una Función
Dominio a partir de gráfica
Determina el dominio de las funciones representadas en las siguientes gráficas:
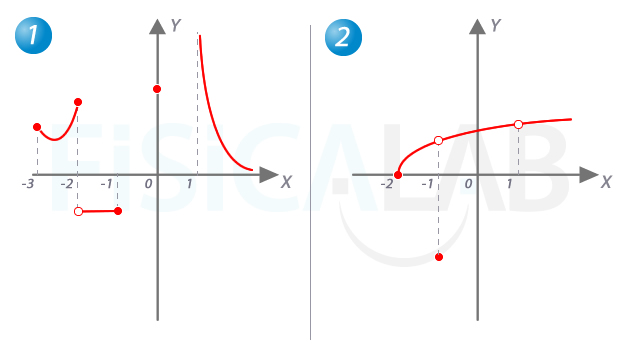
Dominio de funciones racionales
Calcula el dominio de las siguientes funciones racionales.
Dominio de funciones irracionales
Calcula el dominio de las siguientes funciones con raíces.
Dominio de funciones logarítmicas
Calcula el dominio de las siguientes funciones con logaritmos.
Dominio de funciones a trozos
Calcula el dominio de las siguientes funciones definidas por partes:
Dominio de funciones trigonométricas
Calcula el dominio de las siguientes funciones trigonométricas.
Calcular dominio
Calcula el dominio de las siguientes funciones.
- La fuerza con la que se atraen dos cargas en función de la distancia que las separa
Recorrido de una Función
Recorrido de una función a partir de gráfica
Determina el conjunto imagen de las funciones representadas en las siguientes gráficas:
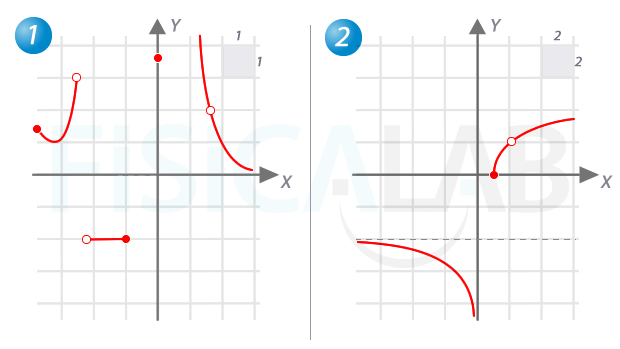
Calcular recorrido de funciones
Calcula el conjunto imagen en las siguientes funciones:
Recorrido a partir de función inversa
Suponiendo que todas las funciones siguientes tienen función inversa, calcula, a partir de ella, el recorrido de las mismas:
Análisis de Funciones
Signo de una función
Estudia los intervalos de signo constante en las siguientes funciones:
Análisis gráfico de funciones
Estudia las funciones representadas en las siguientes gráficas, calculando su dominio, recorrido, monotonía, curvatura, acotación, simetría y periodicidad.
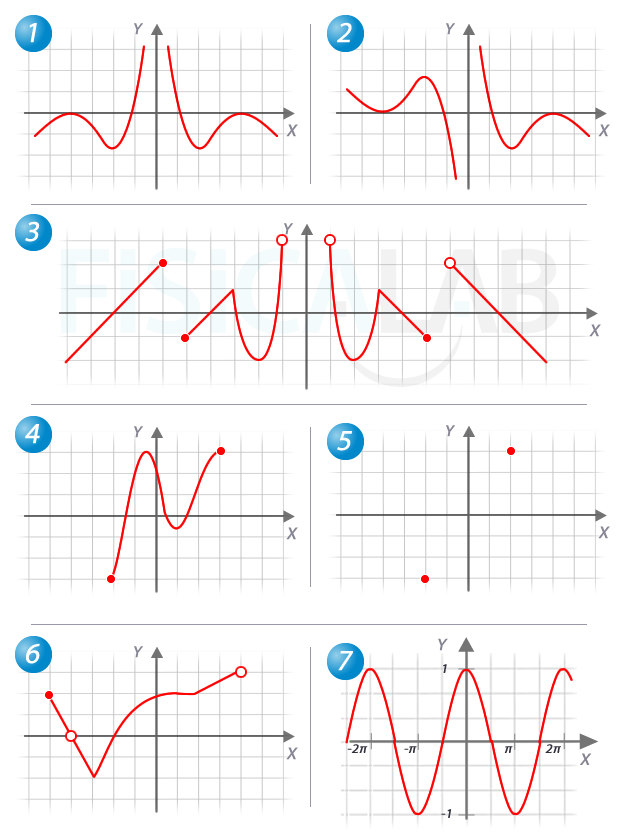
Salvo en el último caso, en el resto puedes asumir que cada cuadro de la cuadrícula tiene una longitud de 1 unidad x 1 unidad.
Simetría de funciones
Determina el tipo de partidad, par o impar, que presentan las siguientes funciones:
Función Definida a Trozos
Gráficas de funciones a trozos
Representa y analiza las siguientes funciones:
Expresión analítica a partir de gráfica de función a trozos
Determina la expresión analítica de las siguientes funciones:
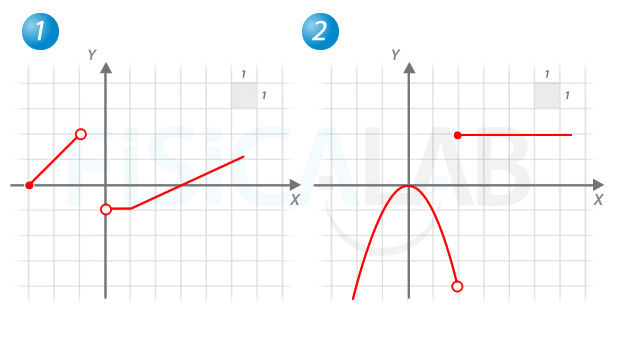
Modelado de situaciones reales con funciones a trozos
Encuentra las funciones reales que sirven para describir las siguientes situaciones:
- La dosis de un determinado medicamente debe comenzar con 6mg el primer día y aumentar 2mg cada día, hasta cumplir la primera semana. A partir de ahí, la dosis se mantiene constante durante otra semana. Finalmente se debe disminuir de manera progresiva hasta desaparecer totalmente en 10 días
- Un móvil parte del reposo y aumenta su velocidad con una aceleración constante de 3m/s2 (es decir, aumenta 3m/s la velocidad cada segundo) hasta llegar a los 18m/s. Ahí permanece 10 segundos y después aplica un frenado que reduce su velocidad a razón 6m/s2
- El precio por aparcar en un determinado parking es de 0.15$/min las dos primeras horas. Luego se reduce a 0.10$/min durante las 3 horas siguientes. Finalmente, el precio se reduce hasta 0.05$/min a partirdel a quinta hora, hasta un máximo de 50$/min por día
Determina, así mismo, el dominio y el recorrido de todas ellas.
Valor Absoluto de una Función
Pasar función a trozos a valor absoluto
Convierte, si es posible, las siguientes funciones definidas por ramas a su forma correspondiente en valor absoluto:
Representación de funciones con valor absoluto
Representa gráficamente las siguientes funciones y obtén su expresión analítica en forma de función a trozos:
Dominio de funciones en valor absoluto
Determina el dominio de las siguientes funciones:
Pasar valor absoluto a función trozos
Define las siguientes funciones en forma de funciones a trozos:
Transformación de Funciones
Transformaciones de puntos de una función
Sabiendo que f(x) pasa por el punto (2,5), di un punto de:
Parámetros función a partir de gráfica
Determina el valor de a y b en los siguientes casos:
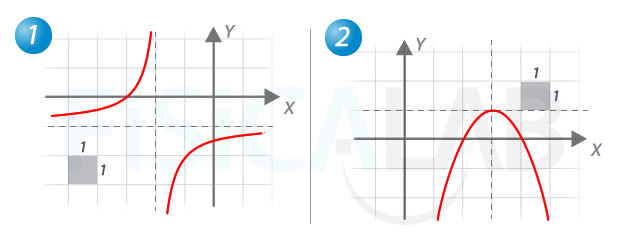
Siendo la función en 1
Transformación gráfica de funciones
1.- Dibuja la gráfica de f(x)=x2. A partir de ella dibuja: a)
2.- Dibuja la gráfica de f(x)=1/x. A partir de ella dibuja: a)
3.- Representa
4.- A partir de la gráfica de la función f(x) de la ilustración:
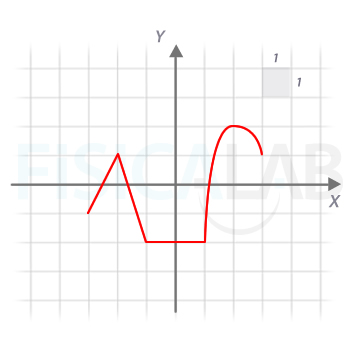
Representa: a) g(x)=-f(-x) ; b) g(x)=3-f(-x) ; c) g(x)=3-f(-2x) ; d) g(x)=3-2·f(-2x-2)
Representación gráfica mediante transformación de funciones elementales
Representa las siguientes funciones mediante las transformaciones de las funciones tipo asociadas:
Suma y Resta de Funciones
Suma y resta de funciones
Realiza las siguientes operaciones, calcula el dominio de la función resultante y determina el elemento simétrico de cada función para la operación suma:
Multiplicación de Funciones
Producto de funciones
Realiza el producto de las siguientes funciones y determina el recíproco multiplicativo de cada una de ellas.
División de funciones
Función Compuesta
Funciones compuestas, tablas y gráficas
A partir de la siguiente tabla, calcula los valores pedidos:
| x=1 | x=2 | x=3 | x=4 | |
| f(x) | 3 | 1 | 2 | 4 |
| g(x) | 4 | 3 | 2 | 1 |
Repite luego el proceso pero considerando los datos de la siguiente imagen, en lugar de los de la tabla:
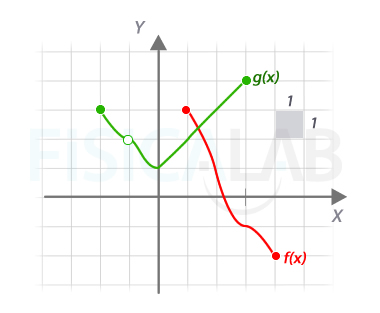
Expresar una función como compuesta
Encuentra las siguientes expresiones a través de la composición de dos funciones distintas:
Encontrar una función componente de la compuesta
Busca la función pedida en cada caso:
Dominio de la función compuesta
Calcula las siguientes funciones compuestas y su dominio:
¿Encuentras algo de especial en este último caso?
Función Inversa
Cálculo de la función inversa
Determina la función inversa de las siguientes funciones:
Comprobar que dos funciones son inversas
Comprueba si las siguientes parejas de funciones son inversas:
En el caso de que sean inversas, comprueba que si el punto (a,b) pertenece a la primera función, entonces el punto (b,a) pertenece a su inversa.
Determina la inversa gráficamente
Determina la gráfica de la función inversa en los siguientes casos:
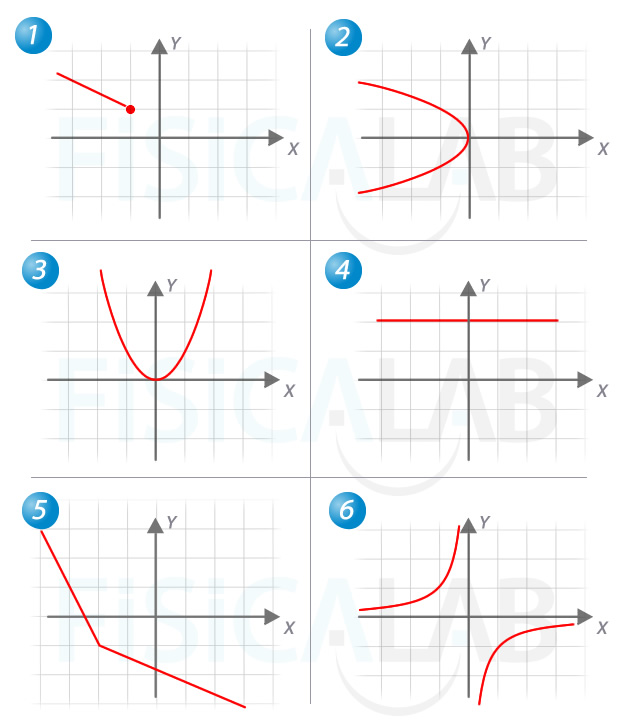
Descomponer función no inyectiva para el cálculo de la inversa
¿Es posible determinar la inversa de la función
¡Suscríbete!
Te ayudamos con contenidos y herramientas para que puedas evaluar a tu alumnado o diseñar tus propias experiencias de aprendizaje.