Descomponer función no inyectiva para el cálculo de la inversa

Consideraciones previas

Recuerda que para que una función tenga inversa, debe ser inyectiva, esto es, a cada elemento del dominio le debe corresponder un único elemento del recorrido.

$$\forall a,b\in Do{m}_f , \text{si} f\left(a\right)= f\left(b\right)\Rightarrow a=b$$

Resolución

Gráficamente podemos comprobar si una función es inyectiva asegurándonos que ninguna recta horizontal la atraviesa en dos puntos. La función del ejercicio es una parábola, y estas no son invectivas.

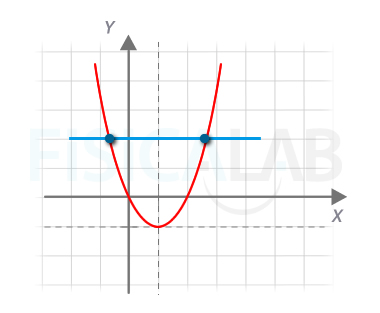
La parábola no es inyectiva

En la figura, representación de la parábola de nuestro ejercicio. Como se pone de manifiesto, no es inyectiva, al cortarla la recta horizontal en dos puntos distintos.

Así, por ejemplo, f(0)=f(2). Si intentásemos calcular la inversa de f por el procedimiento habitual...

$$y={\left(x-1\right)}^2-1\Rightarrow x={\left(y-1\right)}^2-1\Rightarrow {\left(y-1\right)}^2=x+1\Rightarrow y-1=\pm \sqrt{x+1}\Rightarrow y=1\pm \sqrt{x+1}$$

...obtendríamos dos soluciones posibles... con lo que, respondiendo a la primera parte del ejercicio, no es posible calcular la inversa, por que la función no es inyectiva.

Sin embargo, observando la gráfica de la parábola nos damos cuenta que sí que resultaría posible dividirla en dos mitades que sean invectivas.

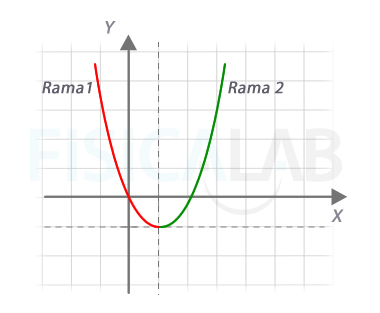
La parábola no es inyectiva

En la figura, representación de la parábola de nuestro ejercicio, pero dividida en dos ramas. La primera, del vértice hacia la izquierda, y la segunda del vértice hacia la derecha.

De esta manera, la función por ramas nos quedaría:

$$f\left(x\right)={\left(x-1\right)}^2-1=\left\{\begin{array}{ccc}{\left(x-1\right)}^2-1& \text{si}& x<x_v\\ {\left(x-1\right)}^2-1& \text{si}& x\ge x_v\end{array}\right.$$

Es una manera alternativa que nos permite, esta vez si, dar una función inversa distinta para cada rama. Comenzamos desarrollando la expresión de la función para calcular x_v:

$$f\left(x\right)={\left(x-1\right)}^2-1=x^2+1-2x-1=x^2-2x\Rightarrow x_v=\frac{-b}{2a}=\frac{2}{2}=1$$

Con lo que nos queda:

$$f\left(x\right)=\left\{\begin{array}{ccc}{\left(x-1\right)}^2-1& \text{si}& x<1\\ {\left(x-1\right)}^2-1& \text{si}& x\ge 1\end{array}\right.\begin{array}{c}\Rightarrow {f_1}^{-1}\left(x\right)=1-\sqrt{x+1}\\ \Rightarrow {f_2}^{-1}\left(x\right)=1+\sqrt{x+1}\end{array}$$

Donde para asociar a cada rama una inversa concreta debemos tener en cuenta que las x<1 se transforman en la función inversa en y<1 y que las x≥1 en y≥1. El resultado final queda: