Transformación gráfica de funciones
Enunciado
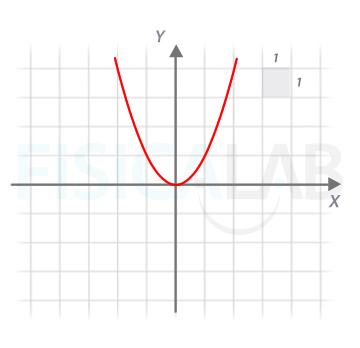
1.- Dibuja la gráfica de f(x)=x2. A partir de ella dibuja: a)
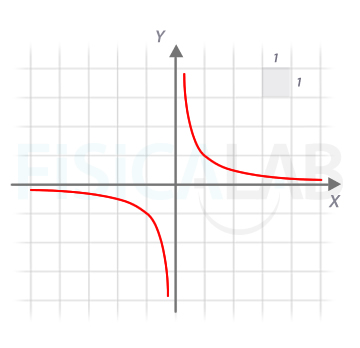
2.- Dibuja la gráfica de f(x)=1/x. A partir de ella dibuja: a)
3.- Representa
4.- A partir de la gráfica de la función f(x) de la ilustración:
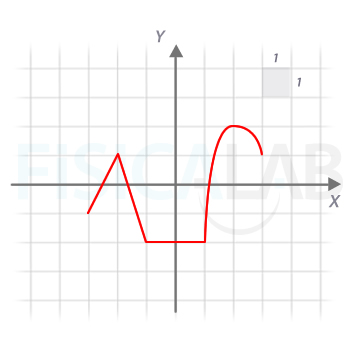
Representa: a) g(x)=-f(-x) ; b) g(x)=3-f(-x) ; c) g(x)=3-f(-2x) ; d) g(x)=3-2·f(-2x-2)
Solución
Resolución
Apartado 1
La gráfica de la función original es una parábola vertical centrada en el origen.
De manera que, en a) tenemos un desplazamiento vertical, en b) un desplazamiento horizontal, en c) una expansión horizontal, y en d) la combinación de una expansión y un desplazamiento horizontales. La ilustración siguiente representa todos estos casos:
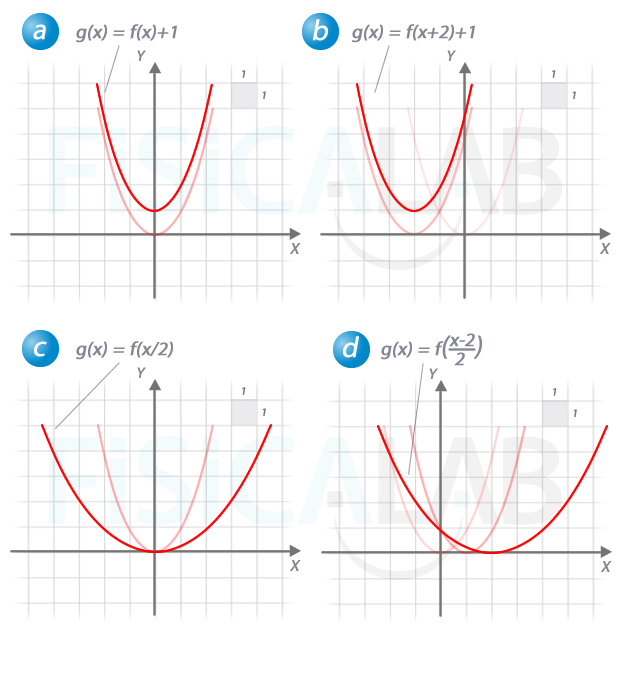
También es interesante escribir la expresión analítica de cada una de estas funciones. Así:
- a) g(x)=f(x)+1=x2+1
- b) g(x)=f(x+2)+1=(x+2)2+1=x2+4x+5
- c) g(x)=f(x/2)=(x/2)2=x2/4
- d)
Merece la pena que observes bien el caso d). Dado que hay que realizar varias transformaciones, el orden es importante, y, si queremos aplicar el visto en teoría, debemos comenzar transformando:
Apartado 2
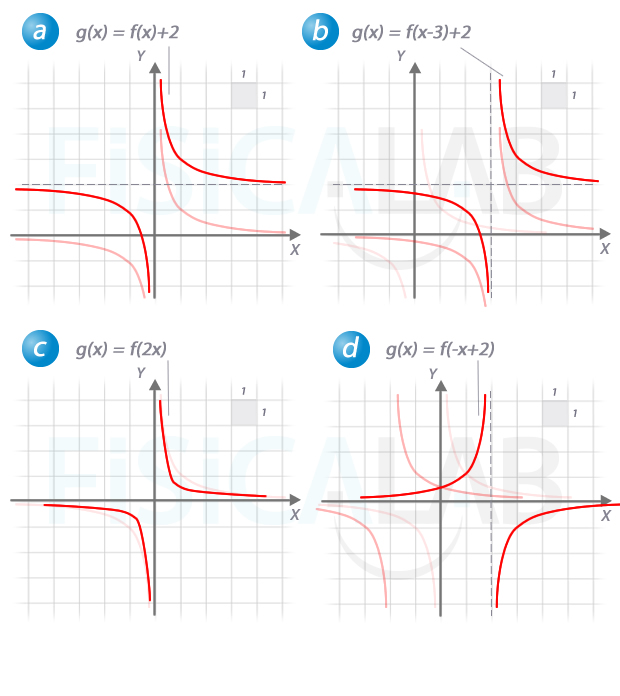
La gráfica de la función original es una hipérbola centrada en el origen.
En este caso cada uno de los apartados contiene la expresión desarrollada, que tendemos que identificar con una de las transformaciones posibles sobre la función original en la forma f(x)+k, f(x+k), etc. Por comodidad vamos a llamar a las nuevas funciones g(x) y a la original f(x). Así tenemos:
Apartado 3
Para llegar a la representación de la función final comenzaremos con
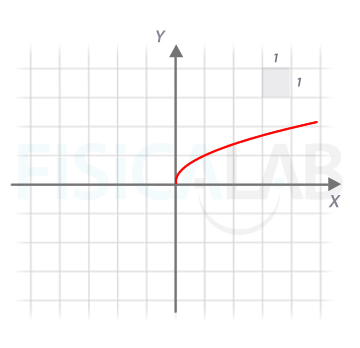
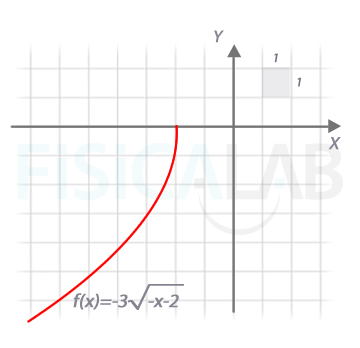
...y realizaremos las transformaciones siguientes:
Así, la representación final queda:
Apartado 4
Partiendo de la función de la ilustración del enunciado, y siguiendo un procedimiento similar al seguido hasta ahora, nos queda:
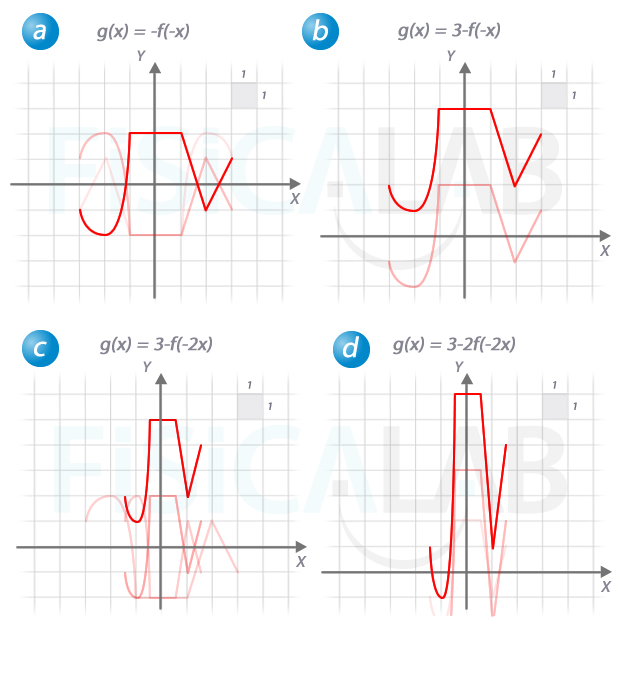
De nuevo, el caso d) es el más dificultoso. Podrías tener la tentación de expandir la función obtenida en el apartado c). Sería un error. Debes seguir el orden propuesto en teoría: comienza por desplazamientos horizontales (en este caso no hay), luego sigue con el resto de transformaciones del eje x, después con las del eje y teniendo presente que la última transformación a aplicar debe ser el desplazamiento vertical.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
