Funciones Arco

En el tema dedicado a trigonometría estudiábamos las razones de un ángulo cualquiera. Estas eran el seno, el coseno y la tangente. A partir de ellas podíamos "construir" las funciones trigonométricas directas, sin más que hacer el ángulo variable (f(x)=sin(x), f(x)=cos(x) ó f(x)=tan(x)). Pues bien, las funciones arco, también llamadas funciones trigonométricas inversas, son el arcoseno, el arcocoseno y el arcotangente. Se construyen haciendo el proceso en el sentido contrario. Veamos:

Funciones directas		Funciones arco
f(x)=sin(x) f(x)=cos(x) f(x)=tan(x)	x → ángulo f(x) → valor razón	f(x)=arcsin(x) f(x)=arccos(x) f(x)=arctan(x)	x → valor razón f(x) → ángulo

Las funciones trigonométricas inversas, o funciones arco, nos proporcionan el valor del ángulo cuya razón es la variable independiente x.

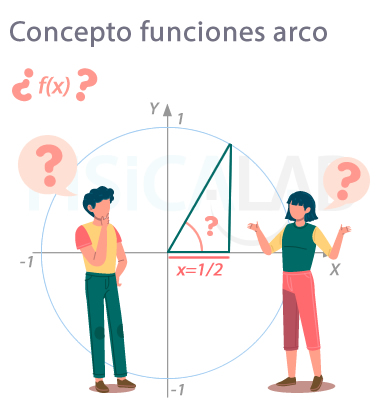
Interpretación geométrica

Observa el triángulo en la ilustración. Desconocemos el valor del ángulo, pero se conoce el valor de su cateto contiguo, x=1/2. Se trata justamente de la proyección sobre el eje x de la hipotenusa de valor 1 inscrita sobre la circunferencia goniométrica. Por ello podemos decir que el ángulo será el "arco cuyo coseno vale 1/2", es decir, el arccos(1/2)=π/3=60º.

Si hacemos el valor del coseno la variable independiente x, y llamamos al ángulo f(x), ya tenemos construída la idea de la función arcocoseno. Para el caso del arcsin y del arctan procederíamos análogamente con las proyecciones en el eje y y con la proyección sobre la recta tangente en el punto (1,0) respectivamente (visita la simulación de definición de razones trigonométricas si no tienes claras estas ideas).

Definiciones, gráficas y características

En la interpretación geométrica que hemos hecho de las funciones trigonométricas inversas nos faltó por revelar una idea que quizás hayas podido adelantar... Si escribimos, por ejemplo, arccos(1/2)=?, en realidad tenemos infinitos valores como resultado, dos por cada "vuelta". Esto es:

arccos(1/2)=π/3 y arccos(1/2)=5π/3 en la primera vuelva
arccos(1/2)=7π/3 y arccos(1/2)=11π/3 en la segunda vuelta (ángulo mayor que 2·π)

...y así sucesivamente. Como ves, son infinitas las posibiliades. Esto sucede también para el arcsin y el arctan. Si recuerdas, al definir las funciones decíamos que a cada valor de x (en este caso 1/2), le puede corresponder, como máximo, un valor de f(x). Es por ello que para hablar de funciones, propiamente dichas, debemos restringir el dominio. En el caso del arccos lo habitual es hacerlo entre [0, π]. Veamos como quedan todas ellas.

Función arcoseno

Definimos la función arcoseno, como la función inversa del seno. A todo x∈[-1, 1] le hace corresponder un valor y∈[-π/2, π/2], con x=sin(y):

$\begin{array}{cccl} f : & [- 1, 1] & \to & [- π / 2, π / 2] \\ x & \mapsto & f (x) = \arcsin (x) \end{array} \begin{matrix} \end{matrix}$

Donde, por definición, el dominio queda [-1,1], y el codominio [-π/2, π/2] (coincide con el recorrido en este caso).

Gráfica de funciones arcoseno y su relación con el seno

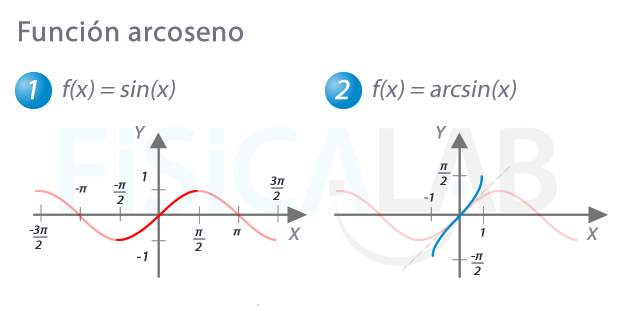
Función arcoseno

A la derecha, en azul, gráfica de la función arcoseno de x. Si restringimos el dominio de la función seno al semiperiodo comprendido entre -π/2 y π/2 a la izquierda en rojo intenso, nos queda una función inyectiva. Podemos apreciar entonces como la función arcoseno, es la inversa del seno, al ser simétricas respecto a la recta y=x marcada a la derecha con una tenue línea gris discontinua.

Otras características:

Continua en (-1, 1)
Creciente en (-1, 1)
Biyectiva, dado que, además de inyectiva (a cada valor de x corresponde un valor de y diferente), es sobreyectiva (todos los valores del codominio [-π/2, π/2] son correspondidos por un valor del dominio, y por tanto el codominio y el recorrido coinciden)
Derivable en (-1, 1), con $f' (x) = \frac{1}{\sqrt{1 - x^{2}}}$
Cóncava en (-1, 0) y convexa en (0, 1), con un punto de inflexión en x=0
Sin asíntotas
Presenta simetría respecto al origen (simetría impar)

Función arcocoseno

Definimos la función arcocoseno, como la función inversa del coseno. A todo x∈[-1, 1] le hace corresponder un valor y∈[0, π], con x=cos(y):

$\begin{array}{cccl} f : & [- 1, 1] & \to & [0, π] \\ x & \mapsto & f (x) = \arccos (x) \end{array} \begin{matrix} \end{matrix}$

Donde, de nuevo, el dominio queda [-1,1], y tanto el codominio como el recorrido quedan esta vez [0, π].

Gráfica de funciones arcocoseno y su relación con el coseno

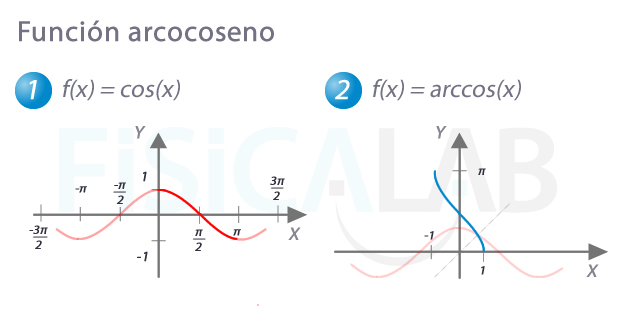
Función arcocoseno

A la derecha, en azul, gráfica de la función arcocoseno de x.Restringiendo el dominio de la función coseno al semiperiodo comprendido entre 0 y π a la izquierda en rojo intenso, nos queda, una función inyectiva. Es el mismo proceso que para la función arcoseno. Así, podemos apreciar como la función arcocoseno, es la inversa del coseno, al ser simétricas respecto a la recta y=x marcada a la derecha con una tenue línea gris discontinua.

Otras características de la función arcocoseno:

Continua en (-1, 1)
Decreciente en (-1, 1)
Biyectiva, al igual que el arcoseno, porque, además de inyectiva, es sobreyectiva
Derivable en (-1, 1), con $f' (x) = - \frac{1}{\sqrt{1 - x^{2}}}$
Convexa en (-1, 0) y cóncava en (0, 1), con un punto de inflexión en x=0
Sin asíntotas
No presenta simetría par ni impar, pero sí respecto al punto (0, π/2), ya que arccos(x)=π-arccos(-x)

Función arcotangente

Definimos la función arcotangente, como la función inversa de la tangente. A todo valor realx∈ℝ le hace corresponder un valor y∈[-π/2, π/2], con x=tan(y):

$\begin{array}{cccl} f : & ℝ & \to & [- π / 2, π / 2] \\ x & \mapsto & f (x) = \arctan (x) \end{array} \begin{matrix} \end{matrix}$

Donde el dominio es cualquier número real, y tanto el codominio como el recorrido quedan [-π/2, π/2].

Gráfica de funciones arcotangente y su relación con la tangente

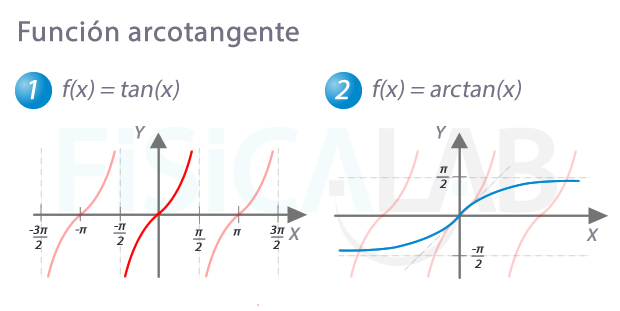
Función arcotangente

A la derecha, en azul, gráfica de la función arcotangente de x. Si restringimos el dominio de la función tangente al semiperiodo comprendido entre -π/2 y π/2 a la izquierda en rojo intenso, nos queda, una función inyectiva. Es el mismo proceso que para las funciones arco anteriores. Así, podemos apreciar como la función arcotangente, es la inversa de la tangente, al ser simétricas respecto a la recta y=x marcada a la derecha con una tenue línea gris discontinua. También podemos apreciar como las asíntotas verticales x=-π/2 y x=π/2, a la izquierda, se convierten en las asíntotas horizontales y=-π/2 y y=π/2 de la función arcotangente.

Otras características:

Continua en ℝ
Creciente en ℝ
Biyectiva, al igual que las demás funciones arco, porque, además de inyectiva, es sobreyectiva
Derivable en ℝ, con $f' (x) = \frac{1}{1 + x^{2}}$
Convexa en (-∞, 0) y cóncava en (0, ∞), con un punto de inflexión en x=0
Con asíntotas horizontales en y=-π/2 y en y=π/2
Presenta simetría impar (respecto al origen)

Una forma alternativa de calcular el valor de la derivada de una función arco, en un punto, si por ejemplo olvidas la expresión correspondiente, es utilizar el procedimiento ya visto en el ejercicio sobre derivadas de las funciones arco.

Notación

Como hemos dicho, las funciones arco son también denominadas en ocasiones funciones trigonométricas inversas por ser las funciones inversas respecto a la operación de composición de las funciones trigonométricas directas correspondientes.

Es frecuente utilizar la siguiente notación para las funciones arco:

Función arcoseno: f(x)=arcsin(x)=sin^-1(x)
Función arcocoseno: f(x)=arccos(x)=cos^-1(x)
Función arcotangente: f(x)=arctan(x)=tan^-1(x)

Esta nomenclatura puede llevar a confusiones con las funciones trigonométricas inversas respecto al producto, también denominadas funciones trigonométricas recíprocas. Recuerda que estas últimas son:

Cosecante: $f (x) = \csc (x) = \frac{1}{\sin (x)}$
Secante: $f (x) = \sec (x) = \frac{1}{\cos (x)}$
Cotangente: $f (x) = \cot (x) = \frac{1}{\cot (x)} = \frac{\cos (x)}{\sin (x)}$

En cualquier caso, nosotros seguiremos habitualmente la norma ISO 80000-2 que fija que las funciones trigonométricas inversas son las inversas respecto al producto (inverso multiplicativo), y por tanto preferimos llamar funciones arco a las inversas respecto a la composición.

Calculadora

Valores arco en calculadora

Para obtener el valor de una función arco, por ejemplo, f(0.5)=arcsin(0.5), utilizamos en la calculadora la tecla de segunda función (normalmente indicada con 2^nd o shift, y el valor correspondiente a la razón (sin^-1 en este caso).

De todas las posibilidades, la calculadora devuelve un valor -π/2<y<π/2 en el caso del arcoseno y el arcotangente, y 0<y<π para el caso del arcocoseno. Se trata justamente de los recorridos de las funciones correspondientes tal y como las hemos definido.

Para estudiar el procedimiento para la obtención de un ángulo conocida su razón, visita el apartado enlazado sobre razones trigonométricas, ya expuestas en un nivel educativo anterior.

Y ahora... ¡Ponte a prueba!

Sobre el autor

José L. Fernández

José Luis Fernández Yagües es ingeniero de telecomunicaciones, profesor experimentado y curioso por naturaleza. Dedica su tiempo a ayudar a la gente a comprender la física, las matemáticas y el desarrollo web. Ama el queso y el sonido del mar.

Apartados relacionados

El apartado no se encuentra disponible en otros niveles educativos.