Teorema de Rolle

El teorema de Rolle establece que:

• Si una función es contínua en un intervalo [a,b]...
• ...es derivable en su interior (a,b), es decir, no presenta picos, y...
• ...tiene el mismo valor en los extremos del intervalo...

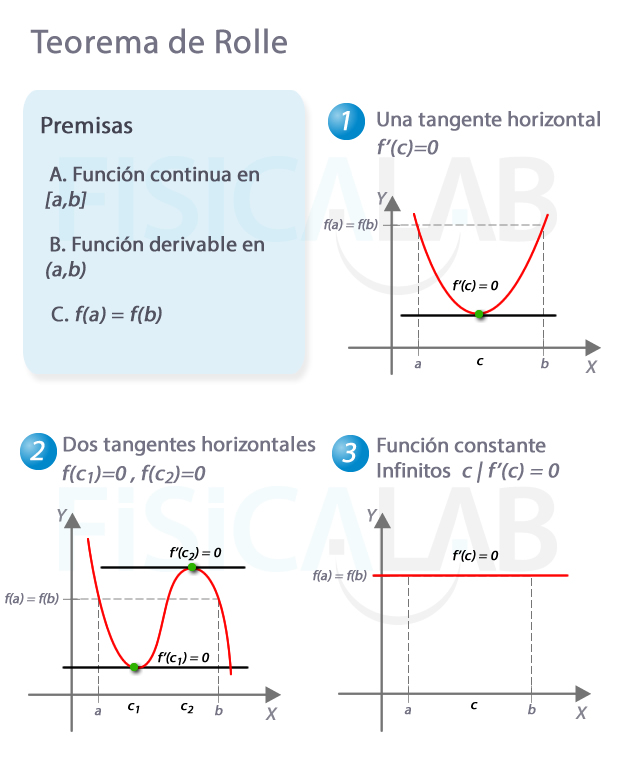
...entonces existe al menos un punto de tangente horizontal.

Gráficas del teorema de Rolle

Las funciones en 1, 2 3 cumplen las premisas indicadas en el teorema de Rolle. Observa que la función en 1 tiene una sola tangente horizontal en (a,b), mientras que la función en 2 tiene 2. Una función constante, como la que aparece en 3 cumple que f'(c)=0 para cualquier c∈(a,b).

Formalmente...

Gracias al teorema de Rolle también podemos afimar que, si en un intervalo (a,b) no existe un valor c que anule la derivada, es porque alguna/s de las hipótesis no se cumple/n. Observa la siguiente imagen:

Contraejemplos

Las funciones en 1, 2 3 no cumplen todas las premisas indicadas en el teorema de Rolle, y en ninguna de ellas hay un f'(c)=0 en el interior del intervalo considereado (a,b). No obstante, debes tener presente que puede haber funciones que no cumplan alguna de las hipótesis del teorema, y sin embargo cuenten con algún valor c tal que f'(c)=0.

Michel Rolle

Michel Rolle (1652 – 1719) fue un matemático francés con importantes trabajos en el campo del análisis. Es reconocido como una de los padres del cálculo infinitesimal debido, precisamente, a su teorema, que formuló sin demostrar a propósito de un problema algebraico-geométrico. Curiosamente fue sus más activos detractores. Según él, el cálculo infinitesimal no era más que una colección de ingeniosa falacias de razonamiento.

Demostración

Partimos de las hipótesis del teorema:

1. La función es continua en [a,b]
2. La función es derivable en (a,b)
3. f(a)=f(b)

Dado que la función es continua en [a,b] (1), por el teorema de Weierstrass, podemos afirmar que alcanza un máximo y un mínimo absoluutos en dicho intervalo. Podemos distinguir dos casos:

• Que bien el máximo o bien el mínimo se encuentren en (a,b). Si llamamos c al valor del máximo o del mínimo, como f es derivable (2), necesariamente por ser un máximo o un mínimo debe cumplirse que f'(c)=0 (tal y como demostramos al hablar de los extremos de una función en un punto en que la función es derivable)
• Que el máximo y el mínimo se alcancen en los extremos del intervalo. Como dichos extremos tienen el mismo valor (3), y son extremos absolutos, necesariamente la función es constante, y el valor de su derivada es 0 en todos los puntos del intervlo