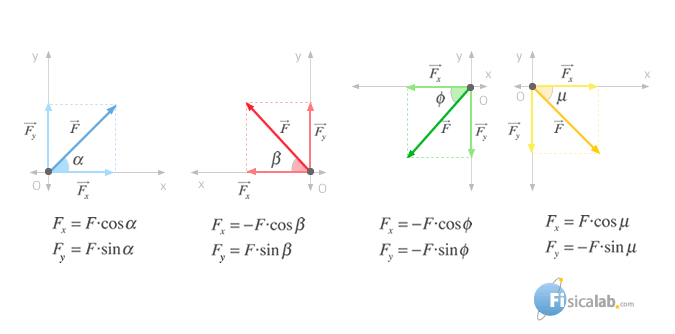
Sometimes, when we study the force acting on a body, it can be interesting to decompose it into several forces, each of them with the direction of the cartesian axis, in sucha a way the effect of all of them is equivalent to the force decomposed. As we study on the section vectors representation, on the plan OXY we get that:
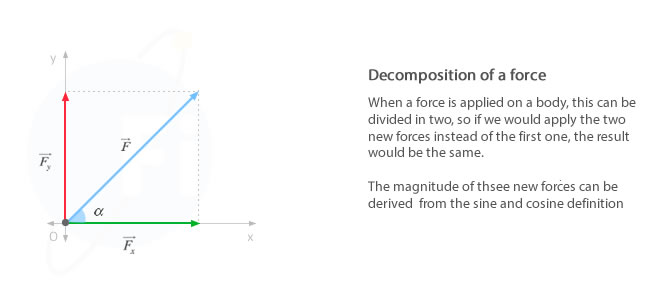
Taking into account the definition of vector magnitude, the magnitude of the force
Throughout the definition of tangent of an acute angle we can relate the magnitudes Fx and Fy to the angle α that take place to with the half turn X positive on the following way:
Additionally we can relate these magnitudes to the lower angle that make