Graphs of Uniform Circular Motion (U.C.M.)

A body performs a uniform circular motion (u.c.m.) when its trajectory is a circumference and its angular velocity is constant. In this section, we are going to study the following graphs:

• Angular position – time
• Angular velocity - time
• Angular acceleration - time

U.C.M. Graphs

Angular position-time (φ-t) graph

$$\boxed{\phi ={\phi }_0+\omega ·t}$$

The angular position–time graph (φ–t) of a uniform circular motion (u.c.m.). represents time on the horizontal axis (t–axis) and angular position on the vertical axis (φ-axis). The angular position, φ, measured in radians according to the units of the international system (S.I.), increases (or decreases) in a uniform manner with the passage of time. We can distinguish two cases, according to whether the angular velocity is positive or negative:

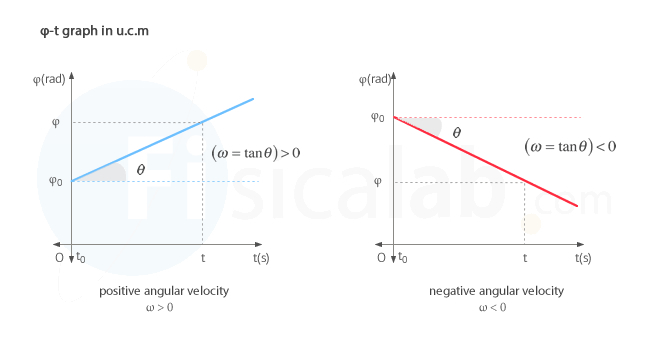
From the angle α, we can get the angular velocity ω. To do it just remember that in a right triangle the tangent of each of its angles is defined as the opposite cathetus divided by the adjacent one:

$$\tan \theta =\frac{\text{opposite\hspace{0.17em}cathetus}}{\text{adjacent cathetus}}=\frac{∆\phi }{∆t}=\frac{\phi -{\phi }_0}{t}=\omega$$

The value of the slope is the value of the angular velocity ω. So, the greater the slope of the straight line, the higher angular velocity ω of the body.

Angular velocity - time (ω-t) graph

$$\boxed{\omega ={\omega }_0=\text{cte}}$$

The angular velocity-time graph (ω–t) of a uniform circular motion (u.c.m.) shows that the angular velocity ω, measured in radians per second (rad/s) according to the international system (S.I.), remains constant over time. Again, we can distinguish two cases:

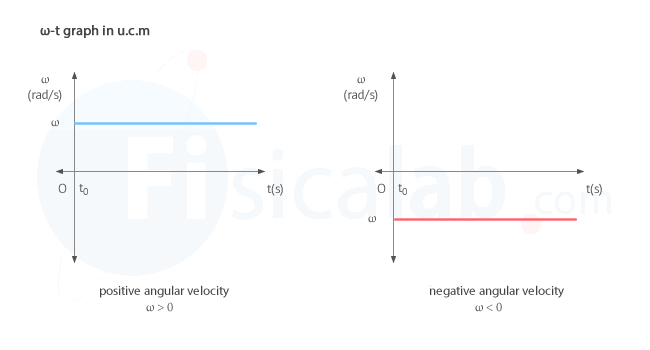
Notice that the area under the curve ω between two instants of time is the angular distance traveled, that is, the angle covered: ∆φ = φ - φ₀).

In this case, it is just the calculation of said area, since it is a rectangle. But, do you know what mathematical tool enables the calculation of the area under a curve, whatever its form?

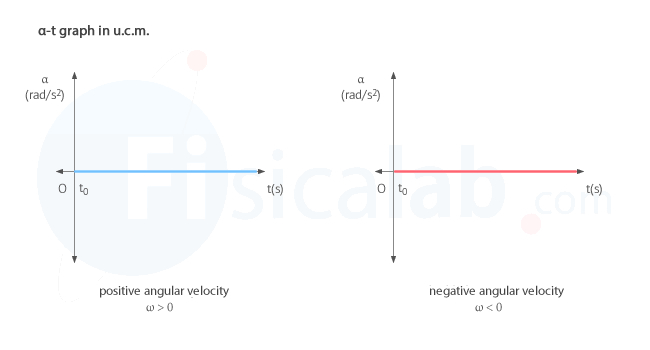
Angular acceleration - time (α-t) graph

$$\boxed{\alpha =0}$$

The angular acceleration-time graph (α-t) of a uniform circular motion (u.c.m.) shows that the angular acceleration, measured in the international system (S.I.) in radians per second squared (rad/s²), is zero at all times. In this case, whether the velocity of the body is considered to be positive or negative, there is only one possibility, as illustrated in the figure: