Continuidad y sus tipos en gráficas
Enunciado
Determina la continuidad de las funciones representadas en las siguientes gráficas, y clasifica las discontinuidades que encuentres.
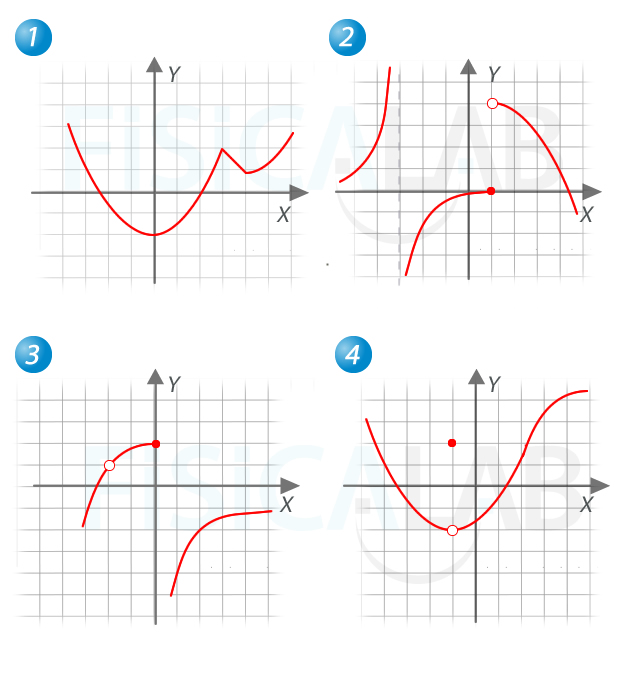
Nota: Considera que cada cuadro tiene una longitud de una unidad de largo y una de alto.
Solución
Consideraciones previas
Gráficamente podemos saber si una función es contínua o no mirando si la podemos "dibujar" con un solo trazado. Te recomendamos que consultes el apartado relacionado para estudiar los distintos tipos de discontinuidad y cómo son gráficamente.
Resolución
La primera función es continua en ℝ: puede ser representada de un solo trazado. Observa que presenta un punto anguloso en x=3 y otro en x=4, pero estos no suponen ningún problema para la continuidad de la función.
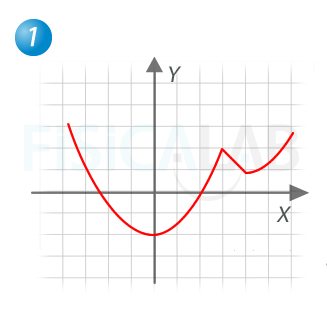
La segunda función presenta varias discontinuidades. La primera, en x=-3. Como puedes ver, se trata de una asíntota vertical, que desde el punto de vista de la discontinuidad es de tipo inevitable de salto infinito. En ese punto se cumple:
La segunda en x=1, es una discontinuidad inevitable de salto finito. Concretamente el salto es de magnitud 4. En ella se cumple:
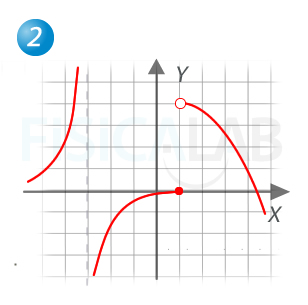
Existen dos discontinuidades. La primera en x=-2, es una discontinuidad evitable. En ella se cumple:
La razón de que la llamemos evitable es que bastaría hacer f(-2)=1 para que la función fuese continua en el punto. Por otro lado, en x=0 hay una asíntota vertical, con lo que se trata de una discontinuidad inevitable de salto infinito. En ella se cumple:
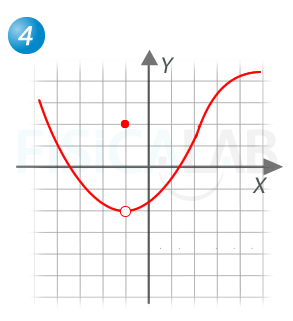
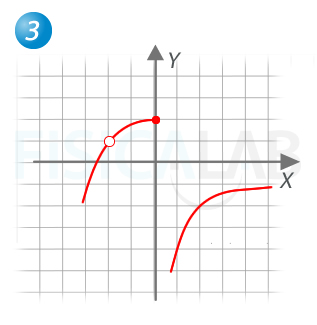
El único punto de discontinuidad está en x=-1. Se trata de una discontinuidad evitable, ya que en él se cumple:
Bastaría hacer coincidir el valor de la función con el del límite para convertir la función en continua (f(-1)=2).
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.
