Monotonía a partir de gráfica de la derivada
Enunciado
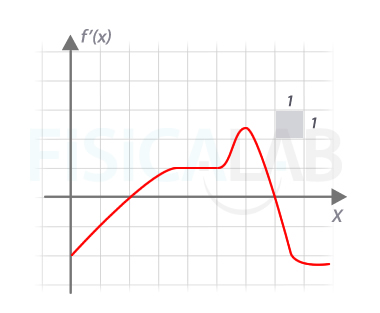
Determina los intervalos de crecimiento y decrecimiento así como los máximos y los mínimos de f(x) a partir de la gráfica de f'(x) siguiente:
Solución
Consideraciones previas
Podemos determinar los intervalos de crecimiento y decrecimiento de una función a partir del signo de su derivada. Además, aquellos puntos en los que la derivada sea 0 son puntos singulares, candidatos a máximos o mínimos según el signo a la izquierda y a la derecha de f'(x).
Resolución
La función f(x) será decreciente en aquellos intervalos en los que f'(x) sea negativa, esto es: (0, 2) y (7, ∞).
La función f(x) es creciente en el intervalo (2, 7) por ser su derivada mayor que cero.
En x=2 la función f(x) presenta un mínimo, al ser f'(2)=0 y ser negativa por la izquierda ( f'(2-)>0 ) y positiva por la derecha ( f'(2+)<0 ).
En x=7 la función f(x) presenta un máximo, al ser f'(7)=0 y ser positiva por la izquierda ( f'(2-)>0 ) y negativa por la derecha ( f'(2+)>0 ).
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.