Regla de L'Hôpital para principiantes
Enunciado
Determina el valor de los siguientes límites:
Solución
Consideraciones previas
Los apartados de este ejercicio están pensados para que practiques de manera directa la regla de L'Hôpital. Esta regla nos permite resolver indeterminaciones del tipo 0/0 o ∞/∞ directamente derivando la función del numerador y del denominador. Concretamente, siempre que las funciones del numerador y del denominador sean derivables en un entorno del punto en el que estamos calculando el límite, se cumple que:
Consulta la teoría vinculada para una información más precisa y formal.
Resolución
1.-
Comenzamos sustituyendo el valor de x correspondiente:
Podemos resolver factorizando numerador y denominador, por tratarse de polinomios, pero vamos a aplicar la regla de L'Hôpital por comodidad, derivando numerador y denominador:
2.-
Seguimos el mismo procedimiento:
Resolvemos la indeterminación aplicando la regla de L'Hôpital:
Hemos obtenido otra indeterminación, de tipo 0/0. ¡No desfallezcamos! Podemos aplicar L'Hôpital reiteredamente, tantas veces como sea necesario:
Por tanto:
3.-
Empezamos normalmente...
...y derivamos para resolver la indeterminación:
4.-
Sustituimos normalmente:
Se trata de un límite que hasta ahora resolvíamos por comparación de infinitos. Sin embargo, en esta ocasión, vamos a aplicar la regla de L'Hôpital.
Se trata del mismo resultado al que habríamos llegado por comparación de infinitos, como no podía ser de otra forma.
5.-
Comenzamos con el procedimiento habitural:
Aplicamos la regla de L'Hôpital para resolver la indeterminación...
6.-
Procedemos normalmente:
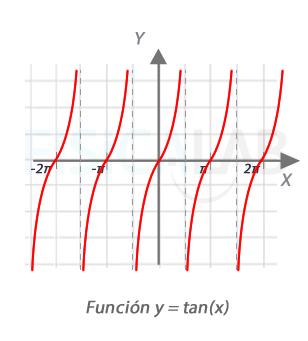
Ten presente que la función tangente se va a infinito precisamente en los múltiplos impares de π/2. Es conveniente recordar su gráfica, ya que si la pones en la calculadora tan(π/2) o tan(5π/2) probablemente obtendrás algo así como Error matemático.
Recordando que D(tan(x))=1/cos2(x), nos queda...
Como hemos llegado a otra indeterminación, podemos resolverla volviendo a aplicar L'Hôpital y teniendo presente la regla de la cadena:
De nuevo una indeterminación que volvemos a intentar resolver aplicando L'Hôpital, esta vez recordando la derivada de un producto:
Por tanto...
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.