Ejercicios Resueltos de Dinámica del Sólido Rígido
Pon a prueba lo que has aprendido en el tema Dinámica del Sólido Rígido con esta lista de ejercicios con sus respectivas soluciones. Consulta:
Ejercicios
Centro de Masas
Centro de masas de 4 partículas en un plano
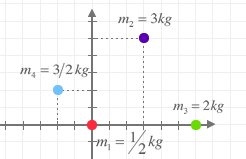
Encuentra el centro de masas de las partículas que aparecen en la figura. Se supone que el sistema es rígido y el sistema de referencia se encuentra expresado en metros.
Velocidad y momento lineal del centro de masas
Estudiamos dos partículas que se mueven en un plano y determinamos que una de ellas tiene una masa de 2 kg y una velocidad de ( 1 , -2 ) m/s y la otra una masa de 3 kg y una velocidad de ( 3 , 1 ). Determina la velocidad del centro de masas del sistema y su momento lineal. ¿Forman parte estas partículas de un sólido rígido?
Centro de masas de varias partículas en movimiento
Tres partículas de masas m1 = 1 kg, m2 = 0.5 kg y m3 = 2 kg se encuentran en movimiento. Sus vectores de posición respectivos son:
- La posición del centro de masas en función del tiempo
- El momento lineal del sistema en t = 2 s
- La fuerza total que actúa sobre el sistema
- La aceleración del centro de masas
Aceleración de sistema de dos partículas dadas sendas fuerzas
Las masas de la figura están unidas por medio de una barra rígida de masa despreciable que se encuentran inicialmente en reposo. Entonces actúan las fuerzas de la figura de manera constante.

Sabiendo que m1 = 2 kg, m2 = 4 kg y los valores de las fuerzas son F1 = 12 N y F2 = 18 N,
- Determina la aceleración del centro de masas del sistema
- ¿Cual es la ecuación del vector de posición del centro de masas en función del tiempo?
Momento Angular
Momento angular rotacional y orbital de la Tierra
Sabiendo que el momento de inercia de una esfera sólida respecto a su eje de rotación viene determinado por la expresión Iesf = 2/5 ·m·r2 , supón que la Tierra es una esfera homogénea de masa 5.972·1024 kg y radio 6371 km y determina:
- Su momento angular rotacional
- Su momento angular orbital alrededor de Sol sabiendo que la distancia media entre este y la Tierra es de 1.496·1011 m
Momento de inercia respecto a distintos ejes
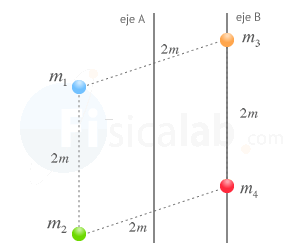
Determina el momento de inercia del sistema de partículas de la figura respecto a cada uno de los ejes representados teniendo en cuenta que m1 = 4 kg ; m2 = 2 kg ; m3 = 3 kg y m4 = 2 kg.
Conservación del momento angular
¿Cuál sería el período de rotación del Sol si colapsara formando una enana blanca de 4000 km de radio, sin variación apreciable de masa?
Datos: Radio solar: 695.800 km ; Período de rotación: 25.4 días ; Momento de inercia de la esfera maciza
Momento angular de un satélite
Determina el momento angular de un satélite que se encuentra a 1000 km sobre la superficie de la Tierra respecto al centro de la misma sabiendo que su masa es de 1200 kg y describe una órbita completa cada 87 minutos. El radio de la Tierra es de 6.37·106 m.
Momento angular de partícula en traslación
Una partícula puntual se encuentra en reposo en la posición
- ¿Cuál es el momento angular con respecto al origen en función del tiempo?
- Determina el momento de fuerza que actúa sobre la partícula en cualquier instante con respecto al origen
Segunda Ley de Newton Aplicada a la Rotación de un Sólido
Segunda ley de Newton aplicada a la rotación de una polea
El señor de la figura aplica una fuerza constante sobre la polea de 40 N. Determina su velocidad angular al cabo de 10 segundos sabiendo que el radio de la polea es de 12 cm, la masa es de 2 kg y el momento de inercia de una polea se puede aproximar por la expresión I = m·r2 .

Rotación del Sólido Rígido
Velocidad centro de masas en yoyó
Determina la velocidad del centro de masas de un yoyó de masa m en función de la altura a la que se encuentra teniendo en cuenta que este se puede considerar un cilindro macizo y por tanto su momento de inercia respecto a su eje de giro se puede calcular según la expresión Iyoyó = 0.5·m·r2 .
Conservación del momento angular en dos cilindros rodantes
Un cilindro se encuentra girando alrededor de un eje vertical sin fricción, con momento de inercia I y con velocidad angular
- Determina la velocidad angular final del sistema
- ¿Qué relación hay entre la energía cinética antes y después de la colisión?
Aceleraciones de cuerpos rodantes en plano inclinado
¿Cuáles son las aceleraciones de descenso de una esfera y un cilindro, ambos sólidos y de la misma masa por un plano inclinado de 20º? Considera que no se produce deslizamiento.
Datos:
- Momento de inercia de un cilindro macizo respecto al eje del cilindro
- Momento de inercia de una esfera maciza respecto a un diámetro
¡Suscríbete!
Te ayudamos con contenidos y herramientas para que puedas evaluar a tu alumnado o diseñar tus propias experiencias de aprendizaje.