Momento de un Vector
El momento de un vector
Momento de un vector respecto a un punto
Se define el momento de un vector
Donde:
La siguiente imagen es una representación gráfica del momento:
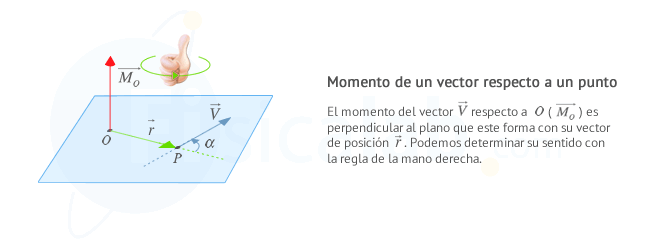
Observa que hemos llamado P al punto de aplicación del vector
Por otro lado, el momento no es más que un producto vectorial. Esto quiere decir que tiene las siguientes características:
- Módulo.
- Dirección. Perpendicular al plano formado por
- Sentido. Para determinarlo puedes usar la regla de la mano derecha: Utiliza la palma de tu mano, orientándola desde
Recuerda que, para el cálculo del producto vectorial, también puedes utilizar su expresión analítica en forma de determinante 3x3, especialmente útil cuando conocemos las componentes cartesianas de cada vector.
Teorema de Varignon
El momento de un vector se puede descomponer en la suma de los momentos de cada una de las componentes de dicho vector. Se trata de la aplicación de la propiedad distributiva del producto vectorial. Así, en el caso de las coordenadas cartesianas, nos queda:
Uso en Física
El momento vectorial es muy importante en Física. Cobra especial relevancia cuando estudiamos la dinámica de un sistema de partículas. En concreto, nos permite conocer el cambio en el estado de rotación de un sólido rígido.
Momento de un vector respecto a un eje
Al momento de un vector respecto a un eje también se le conoce como momento de un vector respecto a una recta y momento áxico.
Se define el momento de un vector
Donde:
La siguiente imagen es una representación gráfica de lo anterior:
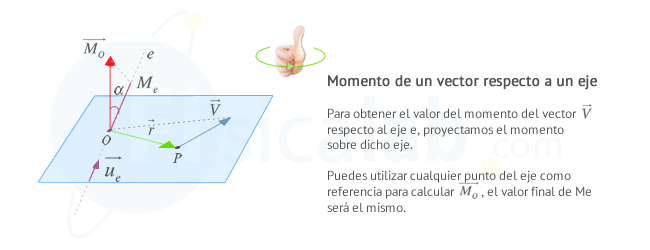
Observa que, de la propia definición, podemos extraer varias conclusiones:
-
Al estar definido a partir de un producto escalar, el momento respecto a un eje es un escalar (una proyección respecto a un eje). En ocasiones, sin embargo, usamos el mismo nombre para referirnos a la magnitud vectorial correspondiente (el vector proyección respecto a dicho eje). Como adivinarás, dicho vector tiene como módulo el del momento del vector respecto al eje y como dirección la que marca el eje. Su expresión en este caso vendría dada por:
-
Es independiente del punto elegido sobre el eje. En el siguiente "Experimenta y aprende" puedes comprobarlo tú mismo
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.