Contraejemplo del teorema de los valores intermedios

Consideraciones previas

Puede que al leer el enunciado pensemos en el teorema de los valores intermedios. Este establece que si una función es continua en un intervalo [a, b] entonces toma todos los valores comprendidos entre f(a) y f(b). En este caso, sabemos que en el intervalo dado toma todos los valores entre 1 y 100, pero claramente no podemos aplicar el camino inverso, es decir, no podemos aplicar dicho teorema porque justamente nos preguntan si se cumple la hipótesis de que sea continua.

Resolución

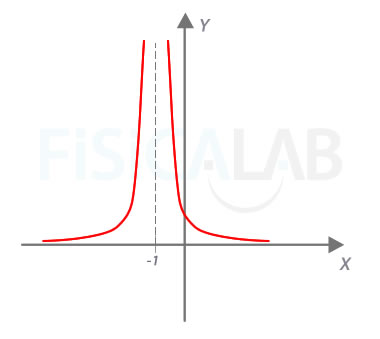
Para demostrar que una cosa es falsa basta con un ejemplo (a veces lo llamamos contraejemplo). En la siguiente gráfica vemos una función que cumple las condiciones y que sin embargo no es continua.

La función es $y={\displaystyle \frac{1}{{(x+1)}^2}}$ que no es continua en x=-1 puesto que se anula el denominador y no pertenece dicho valor al dominio. En x=-2  la función vale 1  y a partir de ahí va creciendo indefinidamente como se obseva en la figura, tomando  todos los valores entre 1 y 100, (y entre uno y cualquier valor suficientemente grande, puesto que a medida que nos vamos acercando a x=-1 por la izquierda la función tiende a infinito).