Razones Trigonométricas de Ángulos que se Diferencian 90º o π/2 rad

En la figura aparecen dos ángulos que se diferencian 90º (o π/2 rad). Son α y β.

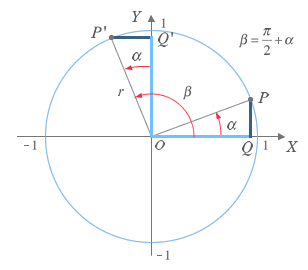
Ángulos que difieren 90º ( π/2 rad )

Siempre que dos ángulos α y β difieran 90º ó π/2 rad se cumple que β - α = 90º ó, lo que es lo mismo, β - α = π/2. De ahí que podamos escribir:

$$\begin{array}{c}\beta =\pi /2+\alpha \\ \beta =90º+\alpha \end{array}$$

En la figura se muestran dos ángulos α y β que se diferencian 90º ó π/2 rad. β esta determinado por el segmento OP' y α por el segmento OP. Si observas bien puedes darte cuenta de que el ángulo β al atravesar el semieje Y positivo crea un triángulo OQ'P' idéntico al triángulo OPQ creado por el ángulo α , por lo que para estudiar las razones trigonométricas del ángulo β podemos utilizar las del ángulo α. 

Así podemos observar que, tal y como estudiamos en el apartado de las razones trigonométricas de cualquier ángulo, la longitud del segmento OQ (cos α) es igual a la longitud de OQ' (sin β) y la longitud de PQ (sin α) es idéntica a la de P'Q' con la diferencia de que al encontrarse en el segundo cuadrante el valor de la abcisa es negativa. Partiendo de estas similitudes podemos establecer que: