Resolución de Triángulos
La resolución de triángulos consiste en hallar sus elementos desconocidos. Es la principal aplicación práctica de la trigonometría y está presente en numerosos campos del conocimiento. Para resolver un triángulo debes conocer al menos 3 de sus elementos, a condición de que no sean los 3 ángulos (pues dos triángulos semejantes diferentes van a tener los mismos ángulos). Por ejemplo, puedes conocer dos lados y un ángulo, dos ángulos y un lado o tres lados (en el caso de los triángulos rectángulos se sobreentiende que uno de los ángulos es de 90º, con lo que sólo es preciso conocer otros dos elementos que no sean los 2 ángulos restantes).
Pasos
- Si es triángulo rectángulo (tiene un ángulo de 90º ó π/2 rad):
Suma de ángulos = 180º
Se utiliza para calcular un ángulo cuando se conocen los otros dos.
Se utiliza para calcular un lado conocidos los otros dos.
Definición de las razones trigonométricas
El seno, el coseno y la tangente de un ángulo se utilizan para relacionar dos lados y un ángulo. Permite despejar uno cualquiera de estos elementos, conocidos los otros dos.
- Si no es triángulo rectángulo:
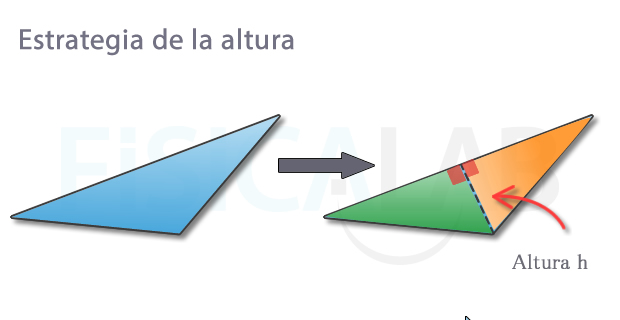
Puedes dividirlo en dos triángulos rectángulos y resolverlos a partir de los pasos ya indicados en el epígrafe anterior, y planteando los sitemas de ecuaciones necesarios.
ó puedes utilizar el teorema del seno o del coseno
Ejemplos
- En este ejercicio resolvemos varios triángulos rectángulos
- En este otro resolvemos varios triángulos no rectángulos a través de la estrategia de la altura
- En este resolvemos varios triángulos no rectángulos mediante la aplicación del teorema del seno y del coseno
Consulta la sección de ejercicios del tema de trigonometría para ver más ejemplos.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.