Estrategia de la altura para resolver triángulos
Enunciado
Resuelve las dos situaciones siguientes aplicando la estrategia de la altura para la resolución de triángulos:
-
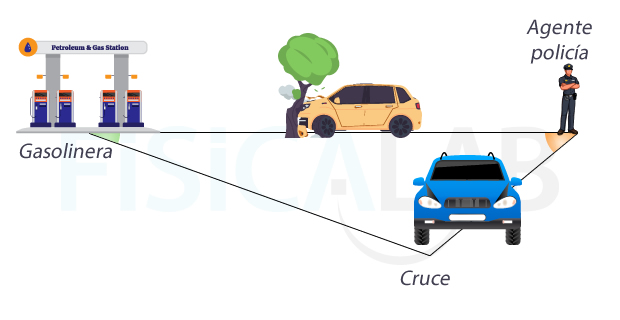
Alba viaja en el coche azul de la figura, con un depósito de gasolina algo escaso. Cuando apenas le queda depósito para recorrer 31 km el policía de la figura le corta el paso, debido a un accidente, y lo redirige a una ruta alternativa. Determina, a partir de los siguientes datos, si Alba llegará a su destino antes de que se vacía su depósito:
- Distancia agente-gasolinera: 30 km
- Ángulo de desvío impuesto por el agente (marcado en naranja): Distancia agente-gasolinera: 40º
- Ángulo de llegada al camino principal después del desvío (marcado en verde): 20º
Observa la siguiente escena (tranquilo, no hemos tenido que maltratar a ningún dragón para la fotografía):
Euclides, de negro, y René, de azul, intentan contener al dragón Albert a la vez que tratan de adivinar su altura. La cadena que sostiene René es de 7.7m y la que sostiene Euclides es de 5.7m. Además, Euclides sabe que el ángulo que forma la cadena con el suelo, marcado en naranja, es de 40º. ¿Podrías echarles una mano a nuestros intrépidos amigos con el asunto de la altura? Y ya que te aplicas... ¿podrías decirme qué distancia separa las dos piedras?
Solución
Consideraciones previas
Se trata de resolver dos triángulos, para lo que seguiremos los pasos indicados en el enlace, aplicando la estrategia de la altura. Recuerda que esta consiste en dividir el triángulo en dos mitades de forma que se puedan aplicar sistemas de ecuaciones a los dos triángulos rectángulos que aparecen.
Como ejercicio propuesto te dejamos que trates de resolver el primer apartado aplicando el teorema del seno.
Resolución
1.-
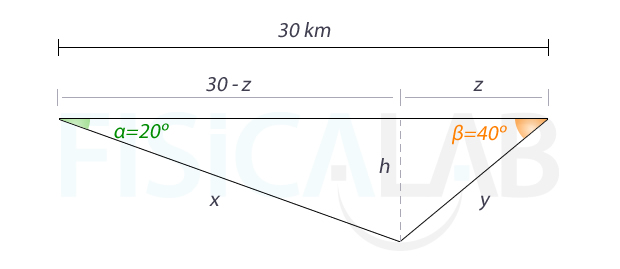
Se trata de un caso en el que se conocen dos ángulos del triángulo y el lado entre ellos. En este caso dividimos el triángulo tal y como se indica en la figura.
Si la distancia x+y es mayor de 31km, Alba no llegará a la gasolinera. Vamos, por tanto, a buscar las relaciones que nos permiten conocer x e y.
Aplicando la definición de tangente
Una vez conocida z, hemos resuelto un cateto en cada triángulo rectángulo. El propio z, y 30-z=20.34km Buscamos las hipotenusas (x e y) de cada uno de ellos a través de la definición de coseno
Por tanto, siendo x+y=34.18 km, mucho nos tememos que Alba no va a poder llegar a la gasolinera y tendrá que andar 3 km a pie para comprar el combustible.
2.-
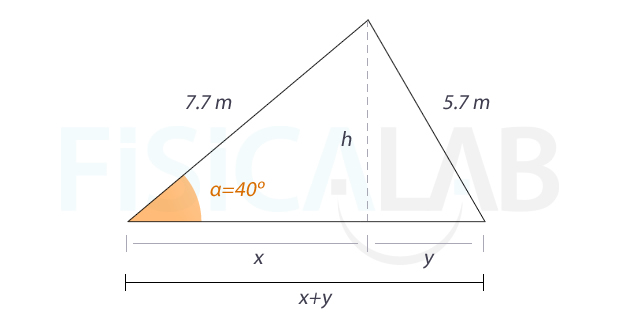
La situación de partida es ahora distinta. Se trata de un caso en el que se conocen dos lados y el ángulo opuesto a uno de ellos. Veamos el triángulo:
Es posible hallar directamente la altura aplicando la definición del seno de un ángulo
Para el cálculo de x podemos aplicar la definición de coseno, la de tangente o bien el teorema de Pitágoras. Vamos por este último camino:
Podemos repetir el mismo razonamiento para calcular y:
Por tanto, la distancia de separación de las dos piedras es x+y=8.74m.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.