Teorema del Seno, Coseno y Tangente
Hasta ahora hemos estudiado las razones trigonométricas para resolver triángulos rectángulos. ¿Pero que ocurre con aquellos que no son de este tipo?. Para responder a esta pregunta se hace uso de lo que se conoce como el teorema del seno y/o el teorema del coseno. En este apartado vamos a estudiar:
Para entender todos ellos adecuadamente ten presente el siguiente triángulo.
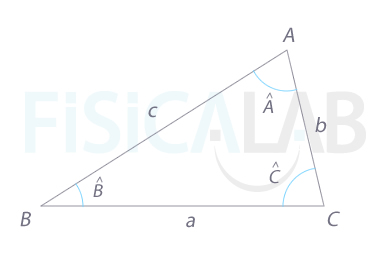
Triángulo cualquiera
En cualquier triángulo los vértices se pueden etiquetar con letras del alfabeto occidental y los ángulos de cada uno de ellos por medio de una letra del alfabeto griego ( α, β, ...) o la letra del vértice con un acento circunflejo ( Â ...)
Teorema del seno
Dado un triángulo cualquiera, las longitudes de sus lados son proporcionales a los senos de los ángulos opuestos.
Demostración
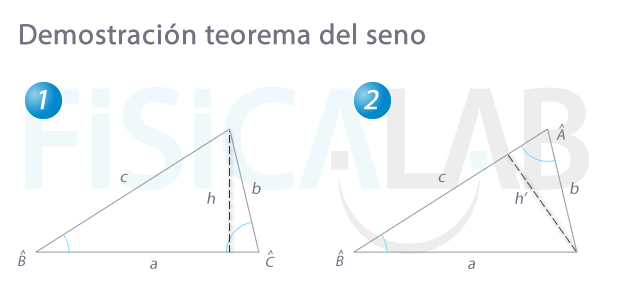
Demostración del teorema del seno
Podemos dividir un triángulo cualquiera, no necesariamente rectángulo, en dos triángulos rectángulos aplicando la estrategia de la altura, consistente en trazar una perpendicular a un lado cualquiera desde el vértice opuesto.
-
Trazando la altura h (perpendicular al lado a) y aplicando la definición de seno, nos queda:
-
Trazando la altura h' (perpendicular al lado c) y volviendo a aplicar la definición de seno, nos queda:
Como se cumplen las dos igualdades anteriores, se cumple:
Casos prácticos
A partir del teorema, podemos obtener las siguientes igualdades:
Estas dan lugar a las siguientes aplicaciones del teorema:
| Tenemos | Nos piden |
|---|---|
| Dos ángulos y un lado opuesto a uno de ellos | El lado opuesto al otro ángulo |
| Dos lados y un ángulo opuesto a uno de ellos | El ángulo opuesto al otro lado |
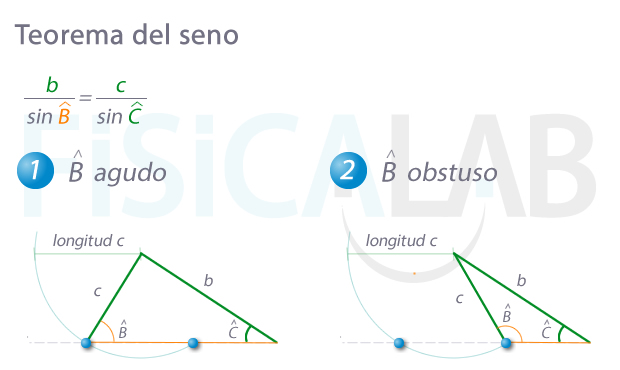
Soluciones posibles en teorema del seno
Dados dos lados de un triángulo b y c, y un ángulo opuesto a uno de ellos, todos en verde, existen dos triángulos posibles obtenidos al aplicar el teorema. El primer triángulo será el asociado a
Esto se debe a que existen dos ángulos cuyo seno tiene el mismo valor, uno en el primer cuadrante y otro en el segundo.
Hemos utilizado el verde para indicar los datos, y el naranja para indicar la incógnita y el lado que esta determina.
Ten presente que, auque no se ha indicado, el ángulo restante se obtiene fácilmente sabiendo que la suma de ángulos de un triángulo suma 180º.
El teorema del seno pone de relieve que, en cualquier triángulo, el ángulo mayor siempre tiene enfrente al lado mayor, y el ángulo menor al lado menor.
Teorema del coseno
Dado un triángulo cualquiera, uno de sus lados elevado al cuadrado es igual a la suma de los cuadrados de los otros lados menos el doble de su producto multiplicado por el coseno del ángulo que forman.
El teorema del coseno puede entenderse como un caso particular del teorema de Pitágoras, y además se demuestra gracias a él, como vamos a ver.
Demostración
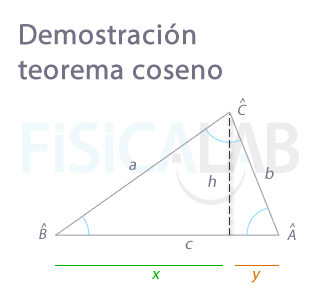
Demostración del teorema del coseno
Considerando el triángulo de lados a, b y c, podemos dividirlo en dos triángulos rectángulos trazando la altura h. Si consideramos el triángulo rectángulo formado por los lados a, h y x, nos queda:
Considerando ahora el triángulo rectángulo de lados b, h e y, tenemos:
Reordenando y aplicando la definición de cos  resulta:
Casos prácticos
Las igualdades del teorema dan luga a las siguientes aplicaciones:
| Tenemos | Nos piden |
|---|---|
| Tres lados | Un ángulo cualquiera |
| Dos lados y un ángulo opuesto a uno de ellos | El otro lado |
| Dos lados y el ángulo que forman | El otro lado |
En el tercer caso también es posible, una vez calculado el otro lado, determinar el otro ángulo a partir del teorema del seno.
Teorema de la tangente
Mucho menos conocido que los otros dos, pero igualmente útil.
En cualquier triángulo se cumple que el cociente entre la suma de dos lados (a, b o c) de un triángulo y su resta es igual al cociente entre la tangente de la media de los dos ángulos opuestos a dichos lados y la tangente de la mitad de la diferencia de éstos.
Demostración
Para demostrar el teorema de la tangente hacemos uso del teorema del seno, visto anteriormente. Vamos a demostrar la primera de las igualdades,
Si llamamos x al valor de dicha igualdad...
Quedando la diferencia entre la suma de los lados:
Finalmente, haciendo uso de la siguiente identidad trigonométrica para transformar la suma o resta de senos en productos...
...nos queda:
Casos prácticos
Las igualdades del teorema dan luga a las siguientes aplicaciones:
| Tenemos | Nos piden |
|---|---|
| Dos ángulos y un lado opuesto a uno de ellos | El lado opuesto al otro ángulo |
| Dos lados y un ángulo opuesto a uno de ellos | El ángulo opuesto al otro ángulo |
Una vez más recuerda que, conocidos dos ángulos cualesquiera de un triángulo, es posible calcular el tercero de manera inmediata sabiendo que la suma de todos los ángulos debe ser 180º.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.