Ecuaciones paramétricas de la recta
Ecuaciones paramétricas de la recta conocidos un punto y un vector director
Las ecuaciones paramétricas de cualquier recta r se obtienen por medio de la siguiente expresión:
Donde:
- x e y son las coordenadas de cualquier punto P(x,y) de la recta.
- a1 y a2 son las coordenadas de un punto conocido de la recta A(a1,a2).
- v1 y v2 son las componentes de un vector director
- λ es un valor real que determina cada coordenada P(x,y) dependiendo del valor que se le asigne.
Explicación
Cualquier recta r que puedas dibujar sobre una hoja de papel puede ser determinada analíticamente por medio de punto A que forme parte de dicha recta y una dirección que se puede expresar mediante un vector no nulo
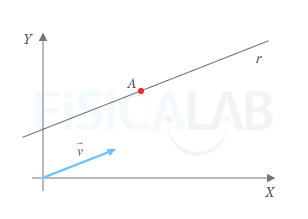
Definición de una recta por medio de un punto y un vector
Como puedes observar en la figura r se trata de una recta que pasa por el punto A y cuya dirección viene dada por el vector
El vector encargado de determinar la dirección de la recta recibe el nombre de vector director y como podrás imaginar este no es único ya que cualquier vector paralelo a este nos sirve también para determinar la dirección de la recta. De esta forma, si

Multiplicación de un número real por un vector cualquiera
Observa en la figura como al multiplicar el vector
Tal y como estudiamos en la ecuación vectorial de una recta, si A(a1,a2) es un punto conocido de una recta r que posee un vector director
De aquí podemos deducir que:
Si a continuación igualamos las componentes a uno y otro lado de la ecuación obtenemos lo que se denominan ecuaciones paramétricas de la recta.
Ecuaciones paramétricas de la recta conocidos dos puntos de la misma
Si en vez de conocer un punto A y un vector director v de una recta conocemos al menos dos puntos de la misma A y B, también podremos calcular su ecuación paramétrica. Para ello, basta con utilizar ambos puntos para calcular un vector director aplicando la propia definición de vector. De esta forma, un posible vector podría ser
Las ecuaciones paramétricas de cualquier recta r se pueden obtener por medio de la siguiente expresión:
Donde:
- x e y son las coordenadas de cualquier punto P(x,y) de la recta.
- a1 y a2 son las coordenadas de un punto conocido de la recta A(a1,a2).
- b1 y b2 son las coordenadas de otro punto conocido de la recta B(b1,b2).
- λ es un valor real que determina cada coordenada P(x,y) dependiendo del valor que se le asigne.
Y ahora... ¡Ponte a prueba!
Apartados relacionados
El apartado no se encuentra disponible en otros niveles educativos.
