Vincular gráficas y expresión analítica en logarítmicas
Enunciado
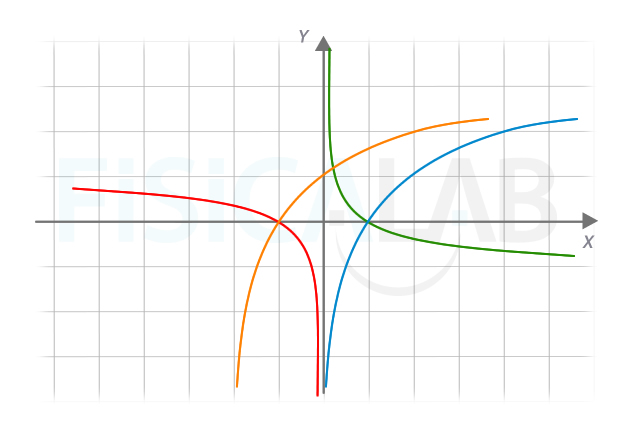
Relaciona cada una de las siguientes expresiones analíticas de funciones con sus gráficas, justificando por qué lo haces:
- f(x)=log2x
Solución
Consideraciones previas
Las funciones logarítmicas presentan algunas características que te van a ayudar a identificarlas en las gráficas. Algunas de las más importantes para la función tipo f(x)=logax son:
- Son crecientes si a>1 y decrecientes si a<1
- Presentan una asíntota vertical en x=0
- Pasan por (1, 0) y por (a, 1)
Recuerda que la función logarítmica es la inversa de las exponencial. Consulta este ejercicio de identificación de funciones exponenciales para encontrar analogías.
Resolución
La función más fácil de identificar es la 4, que corresponde a la gráfica azul. Observa que esta es creciente, y pasa por el punto (2, 1) y (1, 0). Es suficiente para distinguirla del resto.
Por otro lado, la función naranja presenta una forma prácticamente igual pero desplazada dos unidades a la izquierda. Presenta una asíntota vertical en x=-2. Por todo ello la función 3 es la función naranja f(x)=log2(x+2).
De las dos funciones restantes, quizás la 1 sea más sencilla de identificar. Vemos que se trata de la función verde,
La función restante es la 2
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.