Expresión analítica en funciones trigonométricas a partir de gráfica
Enunciado
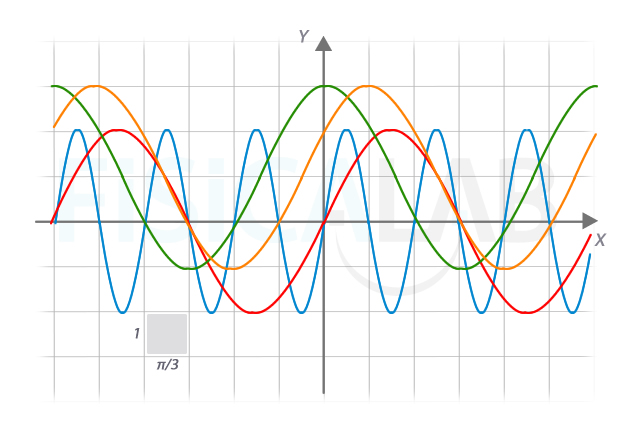
¿Qué expresiones harías corresponder a las siguientes gráficas?
Solución
Consideraciones previas
Las tres funciones tienen forma sinusoidal, por ello se podrán escribir según:
O bien...
Consulta el apartado vinculado para conocer el significado de A, B y C
Por otro lado, nos fijamos que en el eje horizontal cada cuadro corresponde a π/3, y en el vertical a 1 unidadad.
Finalmente, recuerda que las funciones sinusoidales son periódicas, y por tanto podemos describir una misma gráfica con distintas expresiones analíticas. Veamos.
Resolución
Comenzamos por al función en rojo. Vemos que oscila entre -2 y 2. Utilizando el seno
Vemos que f(x)=2·sin(x) se asemeja a la función representada (C=0). También podríamos escribir, por ejemplo, f(x)=2·cos(-x+π/2), ya que sin(algo)=cos(-algo+π/2).
Pasamos a la fución en azul. Vemos que es muy similar a la anterior, pero con una frecuencia mayor. Concretamente utiliza solo 2 cuadros para hacer un ciclo completo. Esto significa que T=2·π/3, y por tanto B=2π/(2π/3)=3. Por otro lado, tiene la misma amplitud que la roja, y podría ser descrita según f(x)=2·sin(3·x).
En relación a la función verde, vemos que se asemeja bastante a la forma de un coseno, pues alcanza su valor máximo en x=0. Utilizaremos la forma de f(x)=A·cos(B·x+C) para describirla. Además, dado que oscila entre -1 y 3, se trata de un coseno desplado. Su amplitud es A=(3-(-1))/2=2. Vemos que su ciclo es de 6 cuadros, por tanto, al igual que sucedía con la función roja, T=2π, y B=1. Con estas ideas podemos escribir f(x)=2·cos(x)+1.
Finalmente, la función naranja, que es igual a la anterior pero desplazada hacia la derecha π/3. Podríamos escribir f(x)=2·cos(x-π/3)+1. También f(x)=2·cos(x-π/3+2π)+1=f(x)=2·cos(x+5π/3)+1 y así sucesivamente, debido a la periodicidad.
Fórmulas
Estas son las principales fórmulas que debes conocer para resolver este ejercicio. Si no tienes claro su significado, te recomendamos que consultes la teoría de los apartados relacionados. Además, en ellos encontrarás, bajo la pestaña Fórmulas, los códigos que te permitirán integrar estas fórmulas en programas externos como por ejemplo Word o Mathematica.