Determinar ángulo a partir de su razón

Consideraciones previas

Ya sabes que para un valor de razón determinado existen dos ángulos posibles, y que la calculadora solo te va a dar uno de ellos. Se hace necesario, por ello, buscar el otro, usando la tabla que vimos en el apartado sobre las razones trigonométricas de cualquier ángulo. El resumen de dicha tabla son las siguientes expresiones:

$$\begin{array}{c}\sin \left(\alpha \right)=\sin \left(180-\alpha \right)\\ \cos \left(\alpha \right)=\cos \left(-\alpha \right)\\ \tan \left(\alpha \right)=\tan \left(180+\alpha \right)\end{array}$$

No obstante, nosotros seguiremos unas orientaciones a partir de gráficas para deducir esos resultados por simple lógica y no tener que memorizar nada.

Vamos a resolver el ejercicio con la calculadora en modo grados sexagesimales, así que asegúrate que las unidades angulares de tu calculadora son tales (debe visualizarse DEG o D).

Resolución

1.-

Nos están pidiendo un ángulo del primer cuadrante. El valor obtenido haciendo sin^-1(0.58) (pulsando SHIFT, SIN y 0.58 en la calculadora) es 35.45º, que es directamente un ángulo del primer cuadrante.

2.-

En este caso el valor devuelto por la calculadora es igual, pero debemos proporcionar como solución un valor de α en el segundo cuadrante. Nos ayudaremos de la siguiente imagen para ilustrar los pasos.

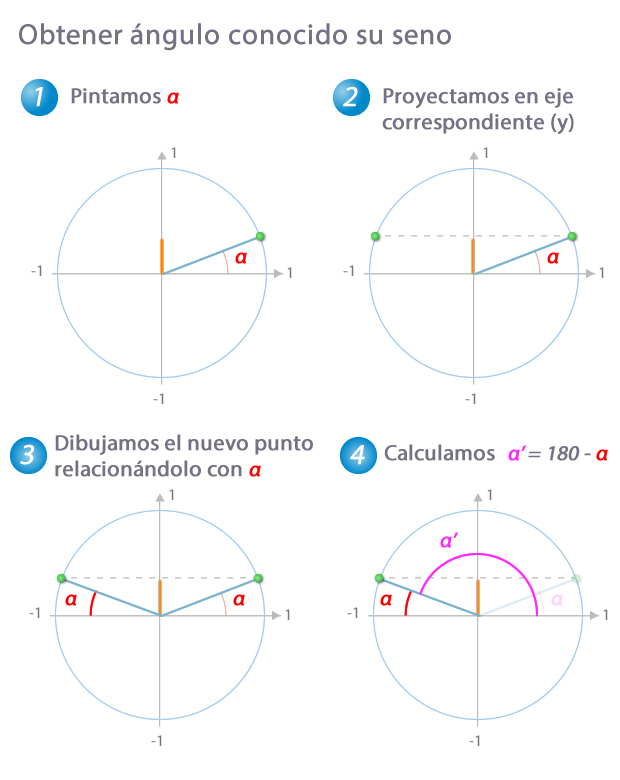
Obtención de α a partir del valor del seno

1. Esbozamos el ángulo obtenido con la calculadora (recuerda que, para el seno, esta nos da valores en el primer o en el cuarto cuadrante siendo α>0 o α<0 respectivamente). No es necesario que seas muy preciso, bastará con que dibujes el ángulo en el cuadrante al que pertenece para que las siguientes deducciones sean correctas
2. Como estamos trabajando con el seno, proyectamos sobre el eje y para buscar el otro ángulo que tiene igual seno
3. Al dibujar el segmento que limita el ángulo, podemos relacionar dicho segmento con α. En este caso nos percatamos que α se encuentra entre la parte negativa del eje x y el segmento que limita el ángulo
4. A partir de ahí resulta inmediato comprobar que el ángulo buscado es α'=180-α

Hemos marcado el valor del seno sobre el eje y, en naranja, para que veas que coincide en α y α'. Observa que el proceso sería similar en cuanto a cálculos si la calculadora nos hubiera devuelto un ángulo en el cuarto cuadrante y tuviéramos que obtener un ángulo del tercero.

Por tanto, el valor de α buscado es α'=180-35.45=144.55º.

3.-

En este caso, al hacer cos^-1(-0.34) la calculadora nos arroja un resultado en el segundo cuadrante: α=109.87. Como nos están pidiendo un valor de ángulo mayor de 180º, suponemos en primer lugar que debe estar en el tercer cuadrante (ya que el coseno de un ángulo, que es su proyección sobre el eje x coinciden en el segundo y en el tercer cuadrante). Nos ayudamos de la siguiente figura para encontrar el ángulo buscado.

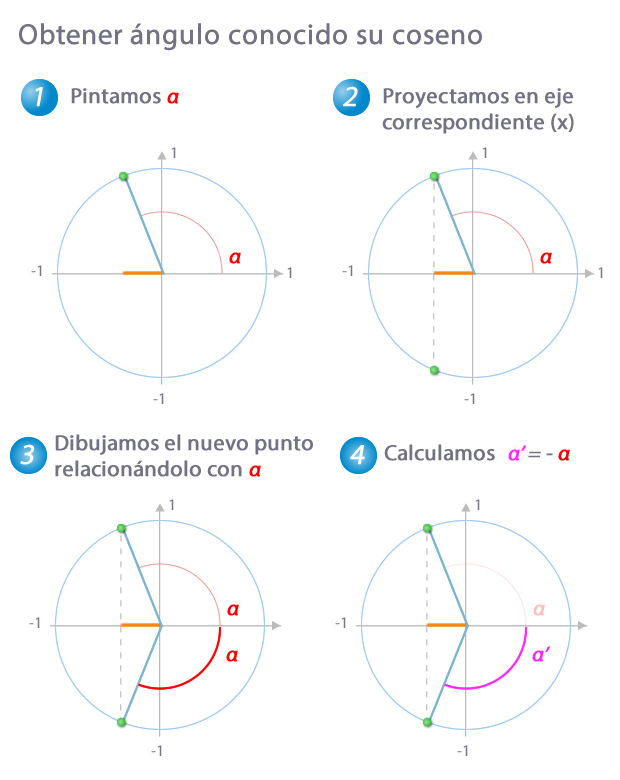
Obtención de α a partir del valor del coseno

1. Esbozamos el ángulo obtenido con la calculadora (recuerda que, para el coseno, esta nos da valores en el primer o en el segundo cuadrante). Al igual que con el coseno, no es necesario que seas muy preciso, basta con que dibujes el ángulo en el cuadrante al que pertenece para que las siguientes deducciones sean correctas
2. Como estamos trabajando con el coseno, proyectamos sobre el eje x para buscar el otro ángulo que tiene igual coseno
3. Al dibujar el segmento que limita el ángulo, podemos relacionar dicho segmento con α. En este caso es evidente que α se encuentra entre la parte postivia del eje x y el segmento que limita el ángulo
4. A partir de ahí resulta inmediato comprobar que el ángulo buscado es α'=180-α

Hemos marcado el valor del coseno sobre el eje x, en naranja, para que veas que coincide en α y α'. Observa que el proceso sería similar en cuanto a cálculos si la calculadora nos hubiera devuelto un ángulo en el primer cuadrante y tuviéramos que obtener un ángulo del cuarto.

Por tanto, el valor de α buscado es α'=-109.87º.. Observa que tenemos que expresar dicho ángulo como α>180º. Para ello sumamos 360º al valor: α=250.13º. ¿Basta con esto? Realmente no, si queremos ser precisos. Hemos dado el único ángulo de primer giro que cumple con α>180º,Por otro lado, y para ser más precisos, tenemos que considerar todos los ángulos que, cumpliendo α>180º,no sean de primer giro. En ese sentido cumplirían tanto los ángulos de segundo como de tercer cuadrante. Por tanto podríamos decir que: α=250.13+360k con k=0,1,2... y que también α=109.87+360n con n=1,2,3....

4.-

En primer lugar tenemos que deducir en qué cuadrante nos están pidiendo el ángulo. Nos dicen que cos(α)<0. Sabemos que el coseno es negativo en segundo y tercer cuadrante. Podría tratarse de cualquiera de los dos. Vayamos a ver qué resultado nos arroja la calculadora (sabemos que será un resultado en el primer o en el segundo cuadrante, porque así opera con el arcotangente). El valor obtenido haciendo tan^-1(1.5) (pulsando SHIFT, TAN y 1.5 en la calculadora) es 56.3º, que es un ángulo del primer cuadrante. Sabemos que el valor de la tangente coincide en primer y tercer cuadrante (también en cuarto y segundo). Ayudémonos de unos esbozos, como hasta ahora, para realizar los cálculos:

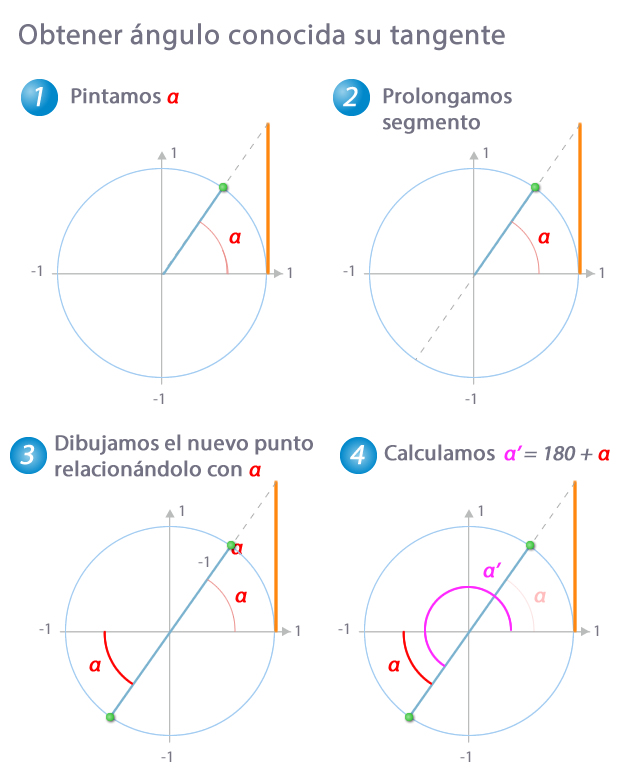
Obtención de α a partir del valor del tangente

1. Esbozamos el ángulo obtenido con la calculadora (recuerda que, para la tangente, esta nos da valores en el primer o en el cuarto cuadrante). Al igual que con el seno y con el coseno, tampoco es necesario que seas muy preciso, basta con que dibujes el ángulo en el cuadrante al que pertenece para que las siguientes deducciones sean correctas
2. Como estamos trabajando con la tangente, prolongamos el segmento que limita α hasta que corte la circunferencia goniométrica, para buscar el otro ángulo que tiene igual tangente
3. Al dibujar el segmento que limita el ángulo, podemos relacionar dicho segmento con α. En este caso es evidente que α se encuentra entre la parte negativa del eje x y el segmento que limita el ángulo
4. A partir de ahí resulta inmediato comprobar que el ángulo buscado es α'=180+α

Hemos marcado el valor de la tangente sobre la circunferencia, en naranja, para que veas que coincide en α y α'. Observa que el proceso sería similar en cuanto a cálculos si la calculadora nos hubiera devuelto un ángulo en el cuarto cuadrante y tuviéramos que obtener un ángulo del segundo.

Por tanto el ángulo buscado en tercer cuadrante sería α'=180+56.3=236.3º. Se trata de un ángulo de primer giro. Cualquier ángulo que sume o reste 360º a α' cumplirá con las dos condiciones impuestas. Por tanto α'=236.3º+k·360 con k=...,-2,-1,0, 1, 2.... Finalmente observa que los ángulos en segundo cuadrante también cumplen que cos(α)<0, pero la tangente en dicho cuadrante es negativa, al ser tan(α)=sin(α)/cos(α) y ser el eje x(coseno) negativo, y el y (seno) positivo. En resumen, no habría que considerar más casos.