Representación función polinómica

Consideraciones previas

Aunque los pasos generales para representar una función son los que puedes encontrar en el apartado enlazado, el proceso se simplifica enormemente en el caso de las funciones polinómicas. Visita este último apartado para profundizar sobre ello.

Resolución

1.-

Por comodidad, conviene empezar estudiando la simetría. Como todos los monomios son de grado impar, la función presenta simetría impar. Efectivamente:

$$f\left(-x\right)=3{\left(-x\right)}^5-5{\left(-x\right)}^3=-3x^5+5x^3=-\left(3x^5-5x^3\right)=-f\left(x\right)$$

Saber que la función presenta simetría impar nos ayudará a representarla más fácilmente, y a evitar errores.

Buscamos ahora las ramas infinitas, que en los polinomios son ramas parabólicas.

$$\underset{x\to \infty }{\lim }3x^5-5x^3=\infty ;\hspace{0.17em}\underset{x\to -\infty }{\lim }3x^5-5x^3=-\infty$$

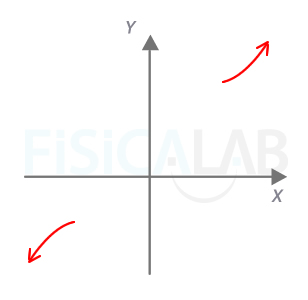
Ramas parabólicas en primer apartado

Las ramas infinitas de la función de este primer apartado se van a menos infinito por la izquierda y a infinito por la derecha.

Buscamos ahora los puntos singulares, es decir, aquellos en los que se anula la primera derivada.

$$f\text{'}\left(x\right)=15x^4-15x^2 ;\hspace{0.17em}15x^4-15x^2=0\Rightarrow x^2\left(15x^2-15\right)=0\left\{\begin{array}{c}x=0\\ x=1\\ x=-1\end{array}\right.$$

Sustituyendo dichas abscisas en la función original, obtenemos los puntos de tangente horizontal.

$$\begin{array}{c}f\left(0\right)=0\\ f\left(1\right)=-2\\ f\left(-1\right)=2\end{array}$$

Observa como el saber que la función presenta simetría impar nos ayuda a detectar posibles errores en el cálculo de puntos singulares. Si x=a es un punto singular, con f(a)=b, entonces x=-a también debe serlo, con f(-a)=-b.

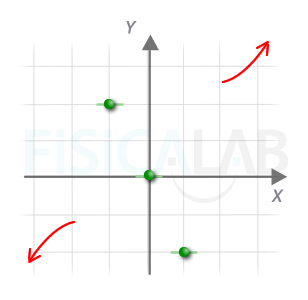
Puntos singulares en primer apartado

Se han representado, en verde, los puntos singulares del polinomio. En ellos la recta tangente (en verde) debe ser horizontal. Estos puntos podrán ser máximos, mínimos o puntos silla. A partir de esta información ya resulta posible trazar mentalmente cómo será la función.

Aunque ya sería suficiente para un esbozo de la función, vamos a estudiar los cortes con los ejes para ser más precisos. Empezamos por el corte con el eje y, haciendo x=0. Efectivamente, se trata del punto singular ya obtenido con anterioridad:

$$f\left(0\right)=3·0^5-5·0^3=0$$

En cuanto al corte con el eje x, hacemos y=0, es decir, f(x)=0, y resolvemos.

$$f\left(x\right)=0\Rightarrow 3·x^5-5·x^3=0\Rightarrow x^3\left(3x^2-5\right)=0\left\{\begin{array}{l}x=0\\ x=\pm \sqrt{\frac{5}{3}}\Rightarrow \left\{\begin{array}{l}x=\sqrt{\frac{5}{3}}\\ x=-\sqrt{\frac{5}{3}}\end{array}\right.\end{array}\right.$$

Hemos obtenido 3 soluciones posibles, esto es, 3 puntos de corte con el eje x, uno de los cuales ya conocíamos (el correspondiente a x=0).

La representación final de la función nos queda:

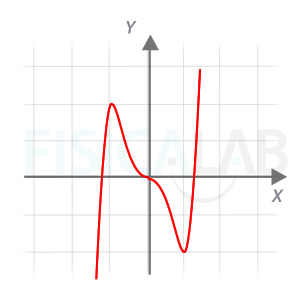
Representación función polinómica 1

Así queda la representación gráfica de la función del apartado 1.

2.-

En este caso, puesto que hay coeficientes pares e impares, no hay simetría.

Vamos a buscar ahora las ramas parabólicas:

$$\underset{x\to \infty }{\lim }\frac{{\displaystyle 8x^3-6x^4}}{{\displaystyle 2}}=-\infty ;\hspace{0.17em}\underset{x\to -\infty }{\lim }\frac{{\displaystyle 8x^3-6x^4}}{{\displaystyle 2}}=-\infty$$

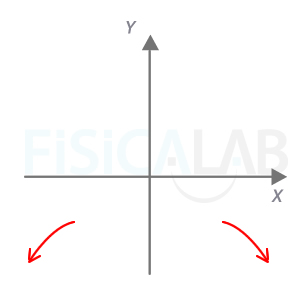
Ramas parabólicas en segundo apartado

Las ramas infinitas de la función de este apartado se van a menos infinito tanto por la izquierda como por la derecha.

Busquemos los puntos singulares, es decir, aquellos en los que se anula la primera derivada. Antes de derivar, por comodidad, arreglamos un poco el polinomio original:

$$f\left(x\right)=\frac{8x^3-6x^4}{2}=\frac{8}{2}{x}^3-\frac{6}{2}{x}^4=4x^3-3x^4\Rightarrow f\text{'}\left(x\right)=12x^2-12x^3$$

Igualando dicha derivada a 0 obtenemos las abscisas buscadas:

$$f\text{'}\left(x\right)=12x^2-12x^3=0\Rightarrow 12x^2\left(1-x\right)=0\Rightarrow \left\{\begin{array}{l}x=0\\ 1-x=0\Rightarrow x=1\end{array}\right.$$

Sustituyendo dichas abscisas en la función original, obtenemos los puntos de tangente horizontal.

$$\begin{array}{c}f\left(0\right)=0\\ f\left(1\right)=1\end{array}$$

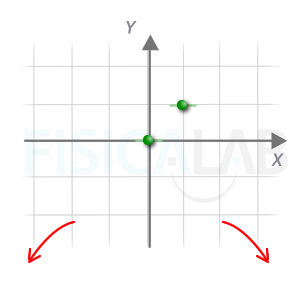
Puntos singulares en segundo apartado

De nuevo hemos representado, en verde, los puntos singulares del polinomio. Como dijimos, en ellos la recta tangente (en verde) debe ser horizontal. A partir de esta información ya resulta posible trazar mentalmente cómo será la función. No obstante, si deseas conocer lo rápidamente que decrece la función a los laterales de los puntos obtenidos, se pueden hallar los puntos de corte y/o hacer una tabla de valores.

Buscaremos los puntos de corte, concretamente los puntos de corte con el eje x nos aportarán algo de la información adicional que necesitamos.

$$0=\frac{8x^3-6x^4}{2}\Rightarrow 0=4x^3-3x^4\Rightarrow 0=x^3\left(4-3x\right)\Rightarrow \left\{\begin{array}{l}x=0\\ x=\frac{4}{3}=1.33\end{array}\right.$$

Observa que uno de los puntos obtenidos es el propio punto singular ya estudiado previamente. Ya estamos en disposición de hacer el esbozo que nos pedían.

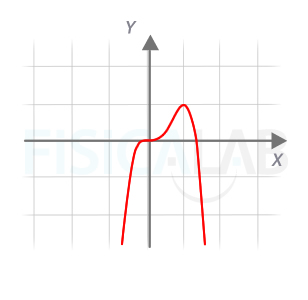
Representación función polinómica 2

Así queda la representación gráfica de la función del apartado 2.

3.-

En este caso, puesto que hay coeficientes pares e impares, la función tampoco es simétrica.

Vamos a buscar ahora las ramas parabólicas:

$$\underset{x\to \infty }{\lim }f\left(x\right)=\infty ;\hspace{0.17em}\underset{x\to -\infty }{\lim }f\left(x\right)=-\infty$$

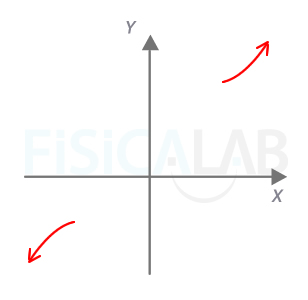
Ramas parabólicas en tercer apartado

Las ramas infinitas de la función de este tercer apartado se van a menos infinito por la izquierda y a infinito por la derecha.

Continuamos con el estudio de los puntos singulares.

$$f\text{'}\left(x\right)=3x^2-6x\Rightarrow f\text{'}\left(x\right)=0\Rightarrow x\left(3x-6\right)\Rightarrow \left\{\begin{array}{l}x=0\\ x=2\end{array}\right.$$

Estas abscisas corresponden a las ordenadas...

$$f\left(0\right)=3\hspace{0.17em}; f\left(2\right)=-1$$

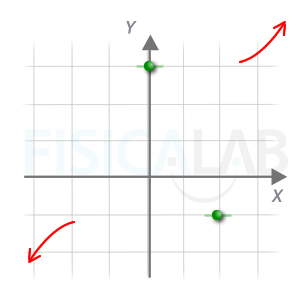
Puntos singulares en tercer apartado

En la imagen hemos representado los puntos singulares correspondientes a la función del tercer apartado. Ya sabes que en ellos la recta tangente (en verde) debe ser horizontal. A partir de esta información ya resulta posible trazar mentalmente cómo será la función. No obstante, para ser más preciso se pueden hallar los puntos de corte y/o hacer una tabla de valores.

Vamos a intentar ahora encontrar los puntos de corte con los ejes. En primer lugar, el punto de corte con el eje y es inmediato. Basta hacer x=0, obteniéndose el mismo punto singular ya encontrado anteriormente (0, 3).

En cuanto a los cortes con el eje x, se trataría de resolver 0=x³-3x²+3. Si probamos a resolverla por Ruffini, probando con divisores de 3 (serían 1,-1,3 y -3), nos percataremos que ninguno de ellos es raíz de la ecuación. ¿Qué podemos hacer?

Si deseas recordar como proceder, te recomendamos que consultes este ejercicio en el que se muestra como aproximar las raíces de un polinomio aplicando Bolzano. Nosotros te dejamos aquí las soluciones, aproximadas hasta las décimas: x=-0.8, x=1.3 y x=2.5. Ya estamos en disposición de esbozar la gráfica final.

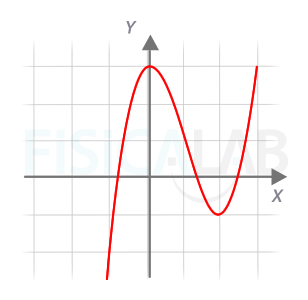
Representación función polinómica 3

Resultado final de la representación gráfica de la función del apartado 3.